4 If the second derivative f '' is negative () , then the function f is concave down ( ) 5 The point x = a determines a relative maximum for function f if f is continuous at x = a , and the first derivative f ' is positive () for x < a and negative () for x > a The point x = a determines an absolute maximum for function f if itIf y = xsqrt(1 x^2) then y^2 = x^2(1 x^2) = x^2 x^4 Now differentiate implicitly 2ydy = (2x 4x^3)dx, therefore, cancel 2s and x and make dy/dx the subject of the formula ydy = (x 2x^3)dx = x(1 2x^2)dx => dy/dx = x(1 2x^2)/y => dy/Jonbenedick shared this question 7 years ago Answered How can you graph the derivative of y=x!?

Derivative Wikipedia
Derivative graph of y=x^3
Derivative graph of y=x^3- Explain how the sign of the first derivative affects the shape of a function's graph State the first derivative test for critical points Use concavity and inflection points to explain how the sign of the second derivative affects the shape of a function's graph Explain the concavity test for a function over an open interval1 Graphing the Derivative of a Function Warmup Part 1 What comes to mind when you think of the word 'derivative'?




Common Derivatives Calculus How To
Desmos offers bestinclass calculators, digital math activities, and curriculum to help every student love math and love learning mathTherefore the graph of the derivative should go through the xaxis at some point As well, looking at the graph, we should see that this happens somewhere between 25 and 0, as well as between 0 and 25 This alone is enough to see that the last graph is the correct answerSimilarly, is the partial derivative of z with respect to y To find this partial derivative, take the derivative of z with respect to y while treating x as a constant Finding Partial Derivatives With z1= x 3 y 3 – 9xy, can be found on the TI with the derivative command
Suppose the curve $ y = x^4 ax^3 bx^2 cx d $ has a tangent line when $ x = 0 $ with equation $ y = 2x 1 $ and tangent line when $ x = 1 $ with equation $ y = 2 3x $ Find the values of $ a,b,c, $ and $ d $ Definition 13 Let f be a function and x = a a value in the function's domain We define the derivative of f with respect to x evaluated at x = a, denoted f ′ ( a), by the formula (134) f ′ ( a) = lim h → 0 f ( a h) − f ( a) h, provided this limit existsPart 2 Graph Then find and graph it Graph of Graph of
Chapter 9 GRAPHS and the DERIVATIVE 194 The answer is all of these are graphs of this same polynomial Graph (a) is for −100Interactive graphs/plots help visualize and better understand the functionsThe first derivative of a continuous function y=f(x) is y'= x(x 30)?



Derivative Calculator With Steps
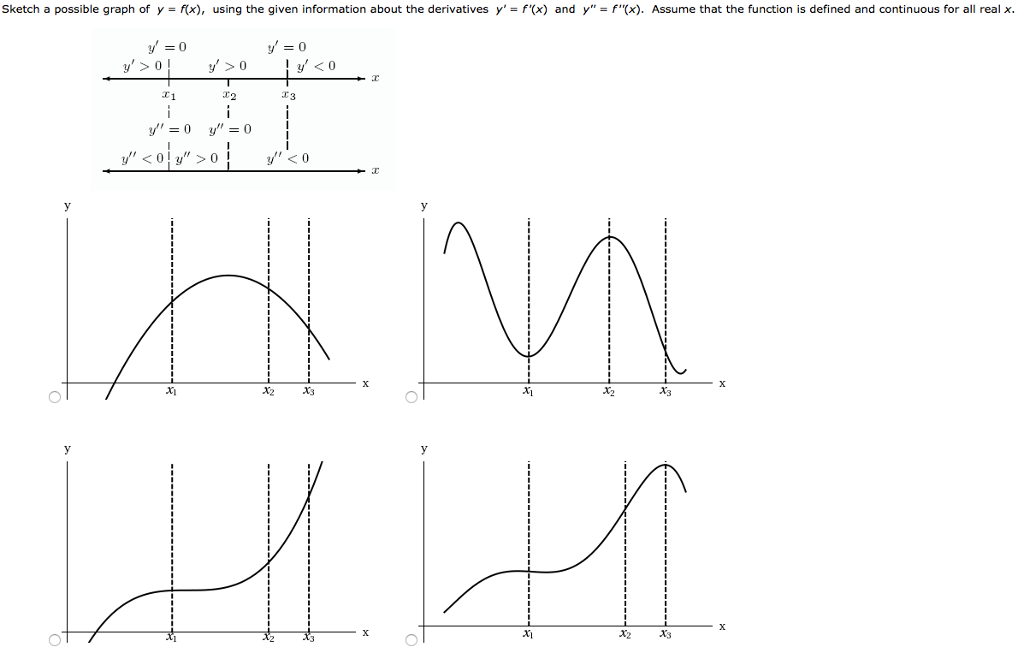



Sketch A Possible Graph Of Y F X Using The Given Chegg Com
Given a function , there are many ways to denote the derivative of with respect to The most common ways are and When a derivative is taken times, the notation or is used These are called higherorder derivatives Note for secondorder derivatives, the notation is often used At a point , the derivative is defined to be It means the slope is the same as the function value (the y value) for all points on the graph Example Let's take the example when x = 2 At this point, the y value is e 2 ≈ 739 Since the derivative of e x is e x, then the slope of the tangent line at x = 2 is also e 2 ≈ 739 x = 2 \displaystyle {x}= {2} x= 2453 Use concavity and inflection points to explain how the sign of the second derivative affects the shape of a function's graph 454 Explain the concavity test for a function over an open interval 455 Explain the relationship between a function and its first and second derivatives 456 State the second derivative test for local extrema




Sketching Graphs Differential Calculus Siyavula
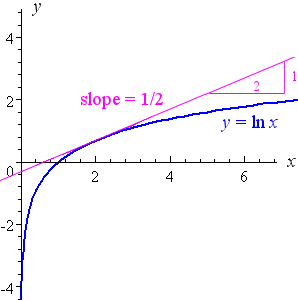



5 Derivative Of The Logarithmic Function
Definition Derivative Function Let f be a function The derivative function, denoted by f ′, is the function whose domain consists of those values of x such that the following limit exists f ′ (x) = lim h → 0f(x h) − f(x) h A function f(x) is said to be differentiable at a if f ′ (a) exists If you do a simple test visually say, the first segment of your reference graph is concave up and positive slope The positive slope notifies that the graph of the derivative will be in the positive terminal The concave up quality of the initial part of the graph assumes that the derivative is increasing The value of is the derivative of y with respect to x, but in this context it is also called the slope of the tangent line So, the derivative of a function at a certain point is the slope of the tangent line that point If we zoom back out again, eventually the graph of no longer looks like a line;




Answered 3 Suppose That The Second Derivative Bartleby
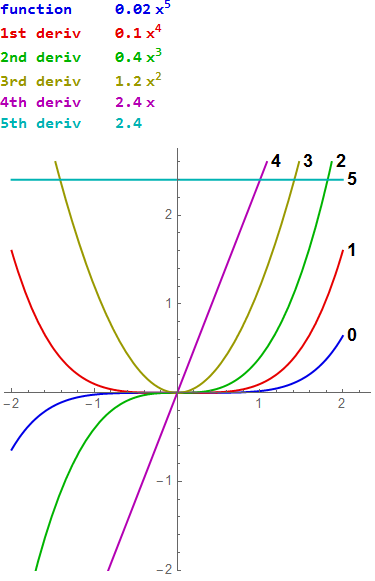



Derivatives
The graphs of a function and its inverse are mirror images across the line y = x If (x, y) is on f(x), then (y, x) is its mirrorimage point across y = x, and the slope of f(x) at x is the reciprocal of the slope of f1 (x) at yGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!To find the equation of the tangent line, we need a point and a slope at that point To find the point, compute f(π 4) = cotπ 4 = 1 Thus the tangent line passes through the point (π 4, 1) Next, find the slope by finding the derivative of f(x) = cotx and evaluating it



Curve Sketching




Common Derivatives Calculus How To
🚨 Hurry, space in our FREE summer bootcamps is running outThe derivative of a functiony= f(x)of a variable xis a measure of the rate at which the value yof the function changes with respect to the change of the variable x It is called the derivativeof fwith respect to x If xand yare real numbers, and if the graphof fis plotted against x, the derivative is the slopeof this graph at each pointThe graph appears but its derivative does not appear I can also attached a point on the curve but I cannot construct a tangent line to it Show translation



How Graphs Of Derivatives Differ From Graphs Of Functions Dummies




Derivative Wikipedia
Motion graphs and derivatives The green line shows the slope of the velocitytime graph at the particular point where the two lines touch Its slope is the acceleration at that point In mechanics, the derivative of the position vs time graph of an object is equal to the velocity of the object In the International System of Units, the Because a function can only have one y for every x, one solution (the negative) has to be omitted This causes the graph of y = x 2 to always be positive If you would plot a graph with both the positive and negative solution of y = x 2, it would look like y = x and y = − x unitedMath 1300 Calculus I The Derivative Function 1The purpose of this problem is to see how to construct a derivative function one point at a time by looking at a graph Background review estimating derivatives, one point at a time The derivative of a function at a point represents the slope (or rate of change) of a function at that point



Derivative Graph Youtube



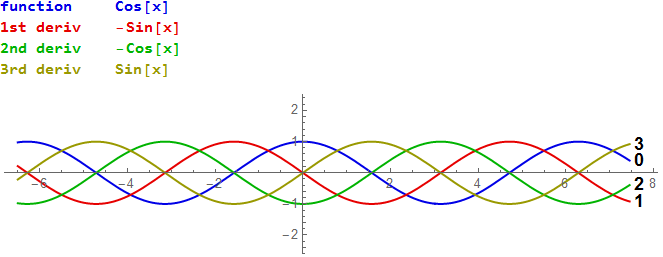
How Do You Graph The Derivative Of F X Cos X Socratic
Derivative of y=x (x^21) \square!The graph of a differentiable function f and its inverse are shown below A point (x,y) has been selected on the graph of f 1 We have that f 1 (x)=y The point (y,x) is on the graph of f, which means that f(y)=x We denote the tangent line to the graph f at (y,x) by M The slope of M is equal to the value of the derivative of f at yThe two graphs are not the same, which is graphical evidence that The Product Rule for derivatives actually says Using this rule to find the derivative of y = x 3 sin x gives Provide graphical support for this derivative Change Y 3 to X^3 * cos(X) 3X^2 *sin(X) Display the graphs in a 3, 3, 1 x 25, 25, 5 window



2




Ac The Derivative Function
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us CreatorsFind y" and then use the graphing procedure to sketch the general shape of the graph of f Y" = 3x2 1x 900 Choose the correct graph below OA OB OC D a 0000 0,000 0000 0000 Q 1See the adjoining detailed graph of f Click HERE to return to the list of problems SOLUTION 2 The domain of f is all xvalues Now determine a sign chart for the first derivative, f' f'(x) = 4x 3 12x 2 = 4x 2 (x 3) = 0 for x=0 and x=3 See the adjoining sign chart for the first derivative, f'




The Graph Of The Derivative Of A Function F X Is Chegg Com
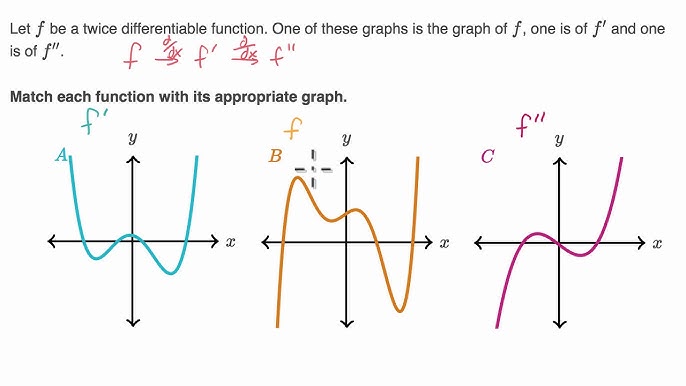



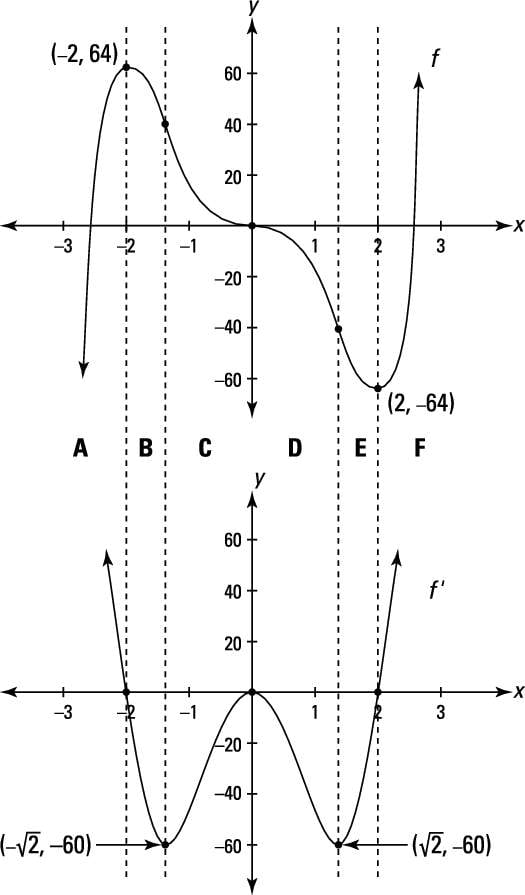
Identifying F F And F Based On Graphs Youtube
Derivative Calculator computes derivatives of a function with respect to given variable using analytical differentiation and displays a stepbystep solution It allows to draw graphs of the function and its derivatives Calculator supports derivatives up toGraph y=x^x by using calculus, x to the x power, tetration functionlimit of x^x as x goes to 0, https//wwwyoutubecom/watch?v=hjEwbzfJFM , derivative of2/21/ Multivariate Calculus Multivariable Functions Havens Figure 1 The graph of the paraboloid given by z= f(x;y) = 4 1 4 (x 2 y2) Vertical trace
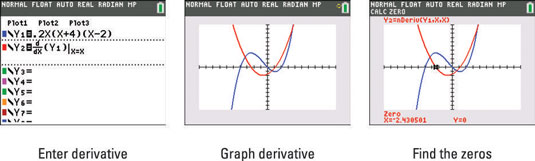



Graph The Derivative Of A Function On The Ti 84 Plus Dummies
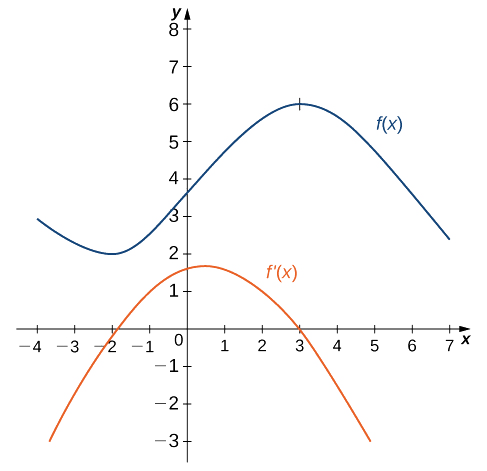



3 2 The Derivative As A Function Mathematics Libretexts
Derivative of y=x Graph the derivative of f(x)=x Then graph y=(x0) /(x0)=x / x What can you conclude?Note that the function defined by y = x x is neither a power function of the form x k nor an exponential function of the form b x and the formulas of Differentiation of these functions cannot be used We need to find another method to find the first derivative of the above function If y = x x and x > 0 then ln y = ln (x x) Use properties of logarithmic functions to expand the right side ofStrictly speaking, the antiderivative is one possible value, whereas the indefinite integral gives all possible values eg antiderivative of x^2 is x^3/3 but the indefinite integral of x^2 is x^3/3 C Well that's what my calculus for dummies book says anyways
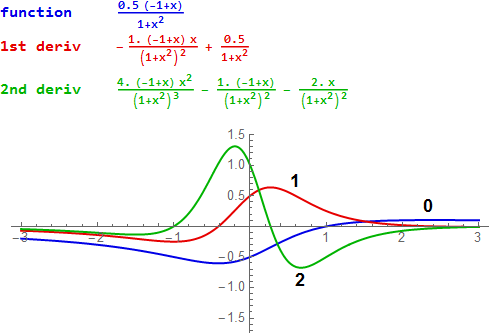



Derivatives
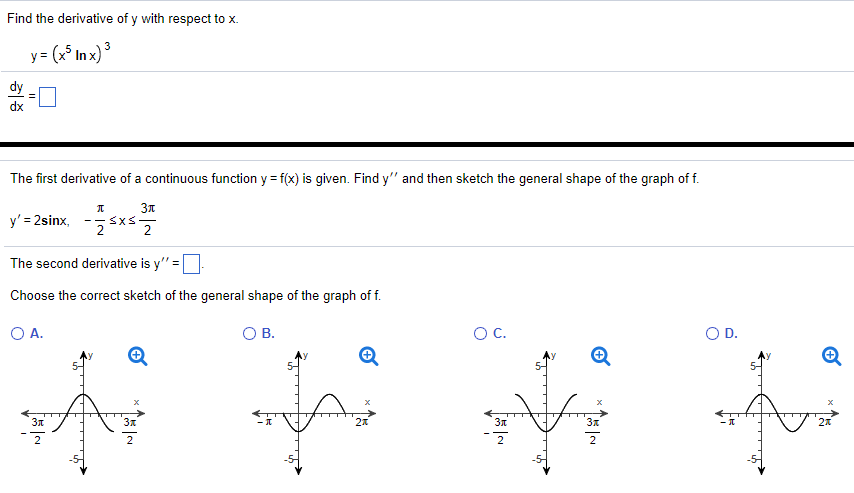



Find The Derivative Of Y With Respect To X Y X 5 Chegg Com
So, taking the derivative of xy tells you just how fast your function is changing at any point on the graph The faster the function's curve goes down or up, the higher the value of its derivativeFind the Derivative f (x)=xe^y f (x) = xey f ( x) = x e y Since ey e y is constant with respect to x x, the derivative of xey x e y with respect to x x is ey d dx x e y d d x x ey d dx x e y d d x x Differentiate using the Power Rule which states that d dx xn d d x x n is nxn−1 n x n 1 where n = 1 n = 1 ey ⋅ 1 e y ⋅ 1 We know the slope of the function is 0 at a handful of points;




The Graph Of Y F X The Derivative Of F X Is Shown Below List The Intervals Where The Graph Of F Is Concave Down 4 2 U 2 4 2 2 4 0 0 4 Study Com



Derivative Of E X Wyzant Lessons
Free derivative calculator differentiate functions with all the steps Type in any function derivative to get the solution, steps and graphThe Derivative Calculator supports computing first, second, , fifth derivatives as well as differentiating functions with many variables (partial derivatives), implicit differentiation and calculating roots/zeros You can also check your answers!First, let us consider the derivative (with respect to x) of xˣ (which I will write as x^x) Let y = x^x Then y = e^ln (x)^x = e^ ln (x)*x, where e is the base of natural logarithms Let u = ln (x)*x




The Derivative Tangent Line Equations Video Khan Academy




Reading The Derivative S Graph Teaching Calculus
to be any number we get the following formula for computing directional derivatives D→uf(x, y) = fx(x, y)a fy(x, y)b D → u f ( x, y) = f x ( x, y) a f y ( x, y) b This is much simpler than the limit definition Also note that this definition assumed that we were working with functions of two variablesDerivative Calculator Step 1 Enter the function you want to find the derivative of in the editor The Derivative Calculator supports solving first, second, fourth derivatives, as well as implicit differentiation and finding the zeros/roots You can also get a better visual and understanding of the function by using our graphing toolWe can see its curvature




Derivative Wikipedia




Common Derivatives Calculus How To
In math, a derivative is a way to show the rate of change or the amount that a function is changing at any given point If you have a function f(x), there are several ways to mark the derivative of f when it comes to xThe common way that this is done is by df / dx and f'(x)If a derivative is taken n times, then the notation d n f / d x n or f n (x) is usedSketch the graph of the given function by determining the appropriate information and points from the first and second derivatives {eq}\displaystyle y= x^3 6 x^2 63 x {/eq}Graph of the derivative of y=x!



5 Derivative Of The Logarithmic Function



Curve Sketching
If the second derivative is zero then the critical point can be anything Below are the graphs of three functions all of which have a critical point at \(x = 0\), the second derivative of all of the functions is zero at \(x = 0\) and yet all three possibilities are exhibited The first is the graph of \(f\left( x \right) = {x^4}\)The graph comes in two parts One part is the line y = x Of course, when y = x then x y = y x We don't even need implicit differentiation to determine the derivative d y d x is equal to 1 along that line But there's still the other curve to deal with In order to take derivatives, it will make it easier if we take logs first Then x y = y Derivatives of Polynomials In the left pane you will see the graph of the function of interest, and a triangle with base 1 unit, indicating the slope of the tangent In the right pane is the graph of the first derivative (the dotted curve)



Derivatives



2



Derivative Function




Content Transformations Of The Parabola
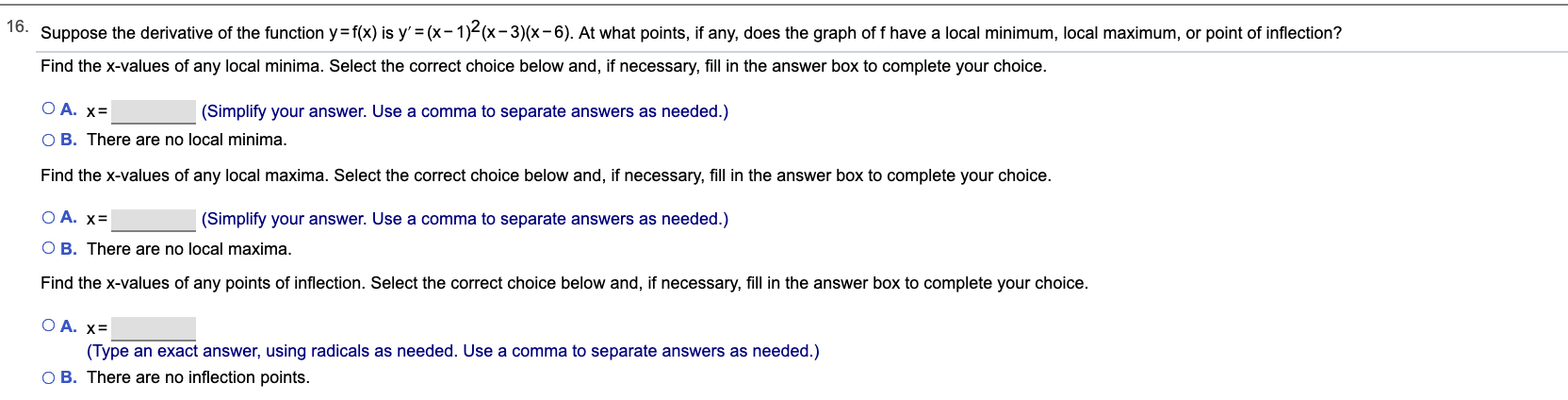



Answered Suppose The Derivative Of The Function Bartleby



Derivatives Of Inverse Functions




5 Derivative Of The Logarithmic Function
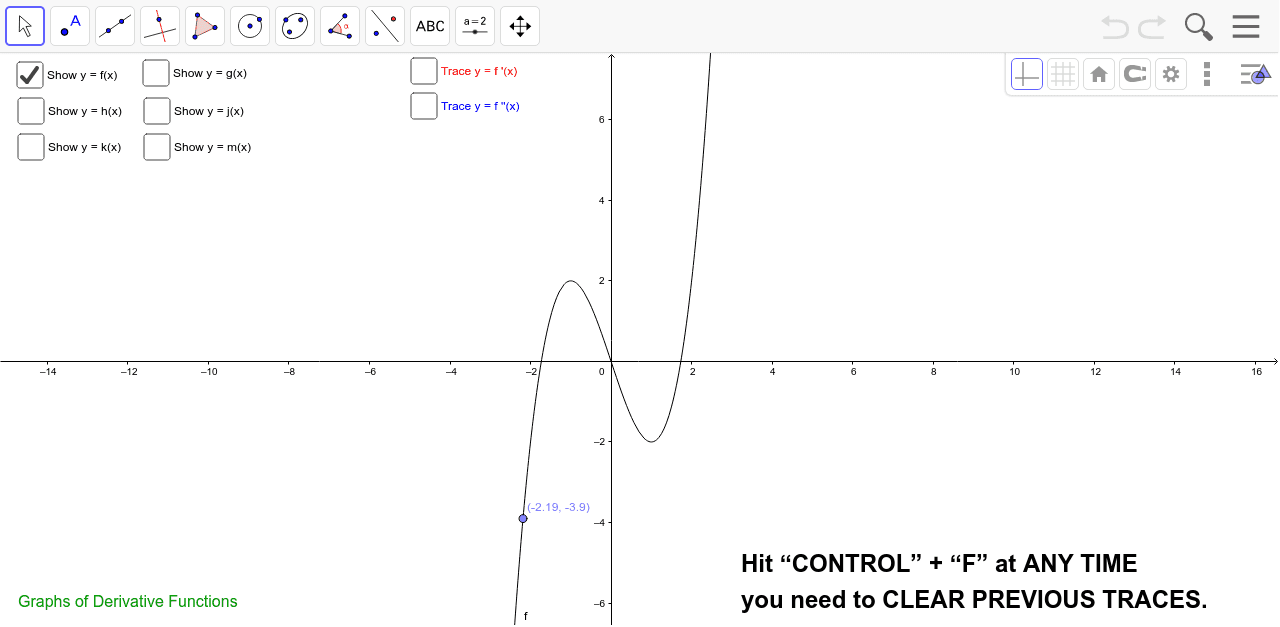



Graphs Of Derivative Functions Geogebra




The Picture Below Shows The Graph Y F X Of The Derivative Of A Function Y F X For Each Of The Brainly Com



What Is The Graph Of The Derivative Of X 2 Quora




Sketching The Derivative Of A Function Youtube
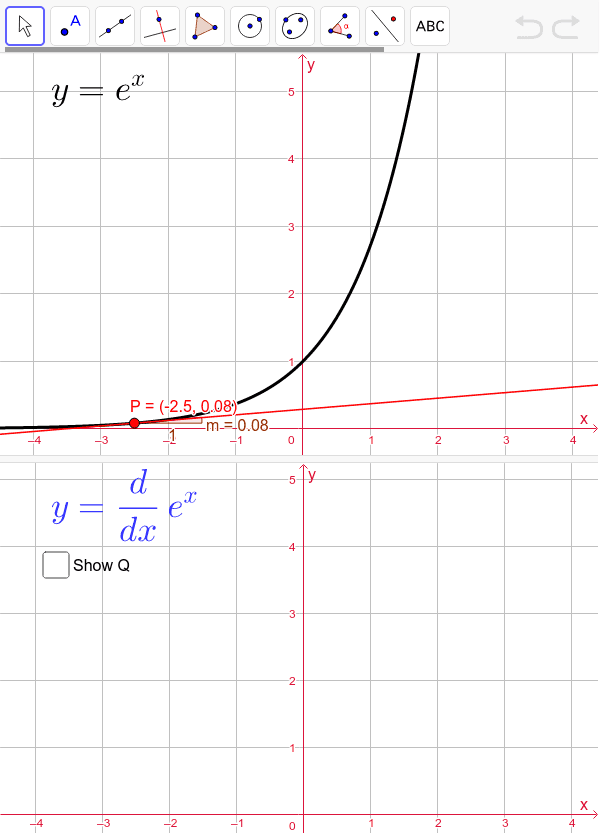



Derivative Of E X Geogebra
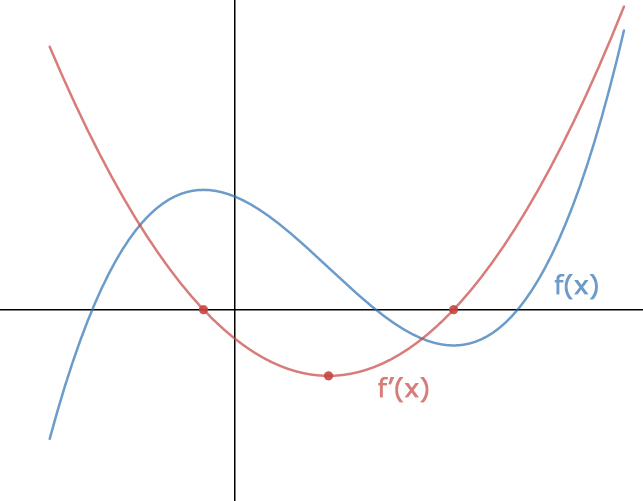



Sketching The Derivative Of A Function Expii
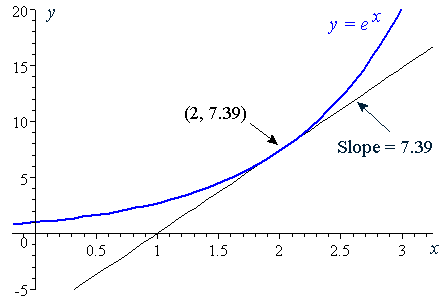



6 Derivative Of The Exponential Function




Derivatives Desmos
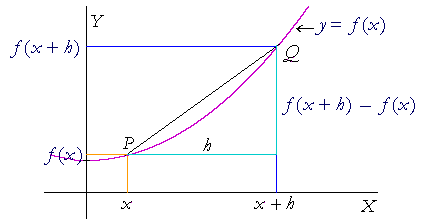



The Meaning Of The Derivative An Approach To Calculus



Implicit Differentiation
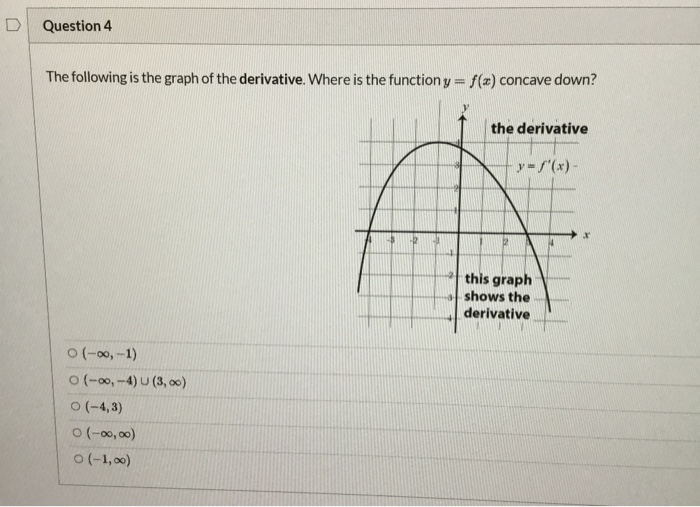



D Question 4 The Following Is The Graph Of The Chegg Com
.gif)



Calculus Differentials And Integrals



1




Solutions To Implicit Differentiation Problems




Derivative Of 𝑒ˣ Video Khan Academy
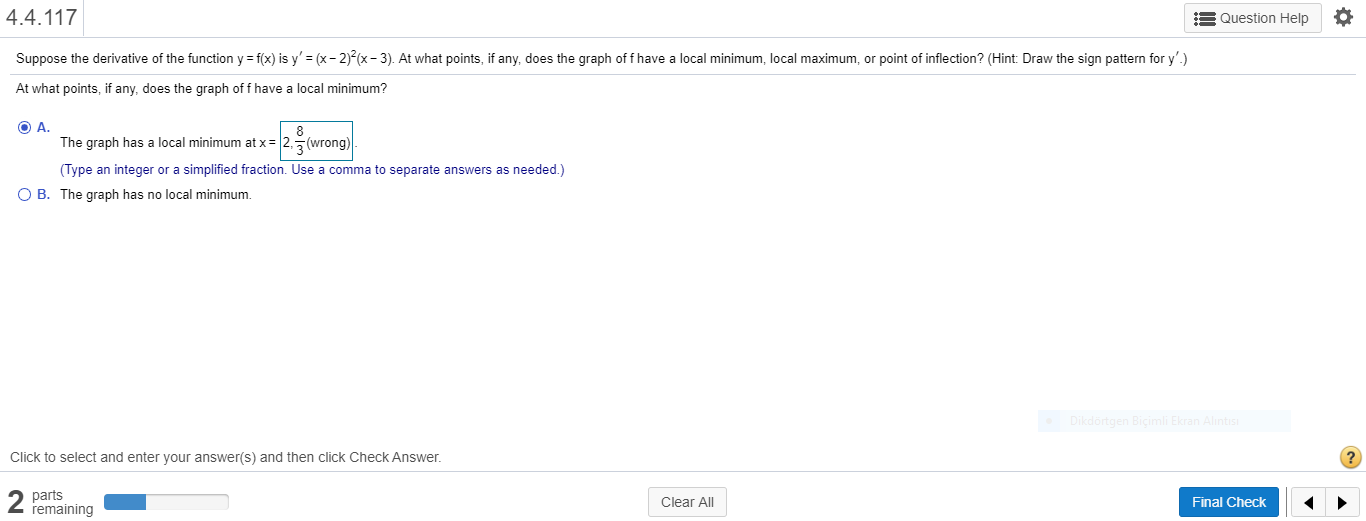



Answered Suppose The Derivative Of The Function Bartleby




Implicit Differentiation
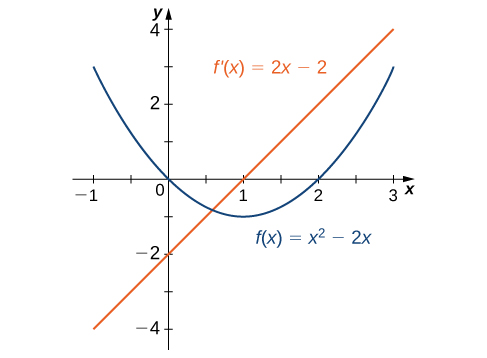



3 2 The Derivative As A Function Mathematics Libretexts




The Graph Of G X Is Given Below Use Your Best Calibrated Eyeball To Find Y 3 If Y Left X G X Right 2 Study Com
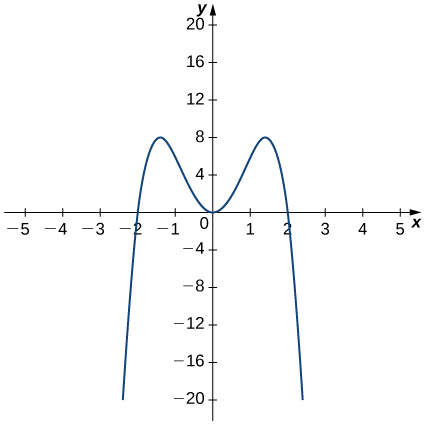



3 2 The Derivative As A Function Calculus Volume 1



Rules Of Calculus Functions Of One Variable




Graphs Of Functions Their Derivatives Study Com



Proof Of The Derivative Of Csc X
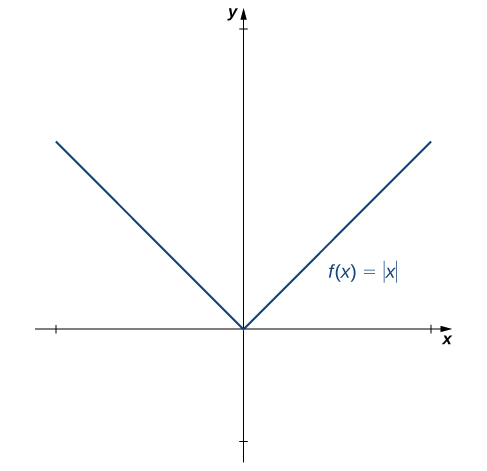



3 2 The Derivative As A Function Mathematics Libretexts



1



2



How To Interpret The Graphs Without The Equations Of A Function And Its First And Second Derivative Quora
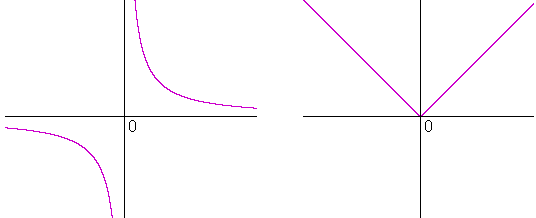



The Meaning Of The Derivative An Approach To Calculus
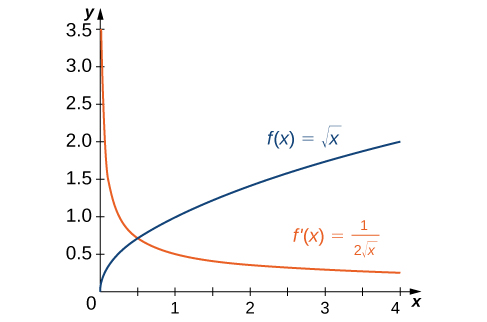



3 2 The Derivative As A Function Calculus Volume 1



Solved The Graph To The Right Shows The Rst And Second Derivative Of A Function Y F X Copy The Picture And Add To It A Sketch Of The Approximate Course Hero




Let Y X 2 3 When Is Y Zero Draw A Sketch Of Y Over The Interval 4 Less Than Or Equal To X Less Than Or Equal To 4 Showing Where The
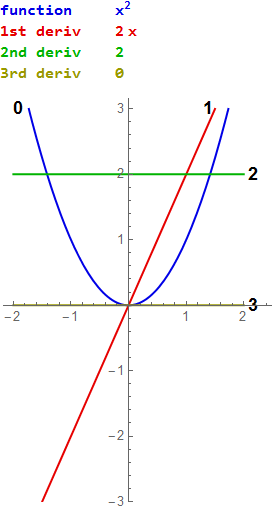



Derivatives
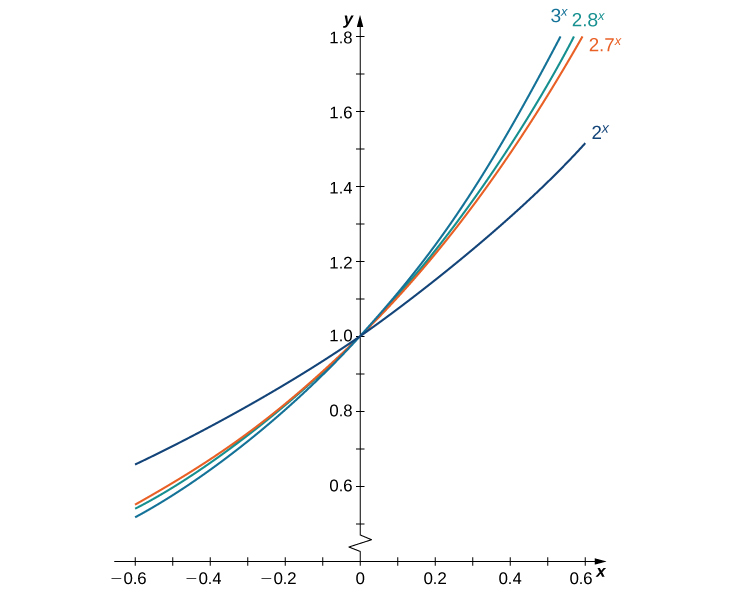



Derivatives Of Exponential And Logarithmic Functions Calculus
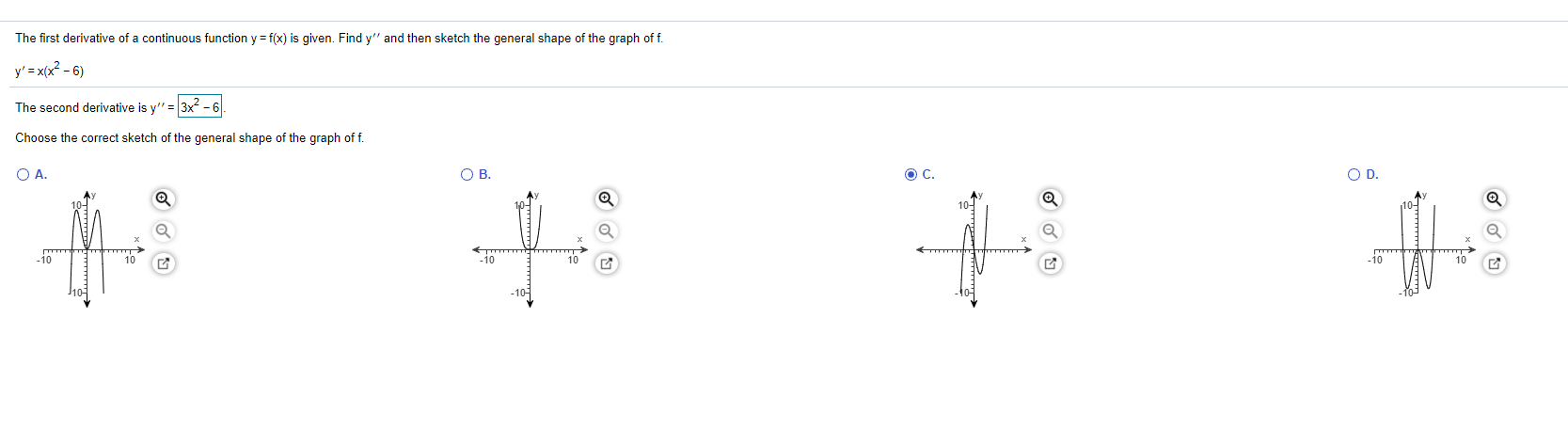



Solved The First Derivative Of A Continuous Function Y Chegg Com



3
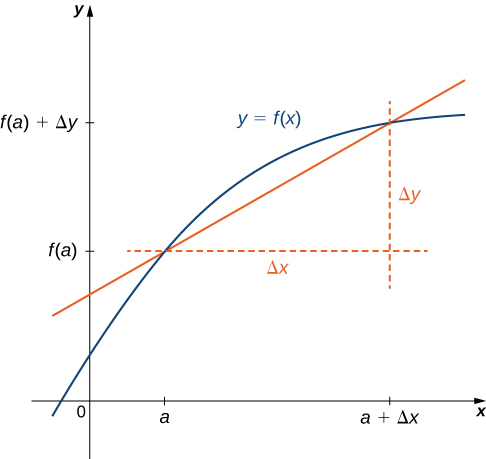



3 2 The Derivative As A Function Mathematics Libretexts
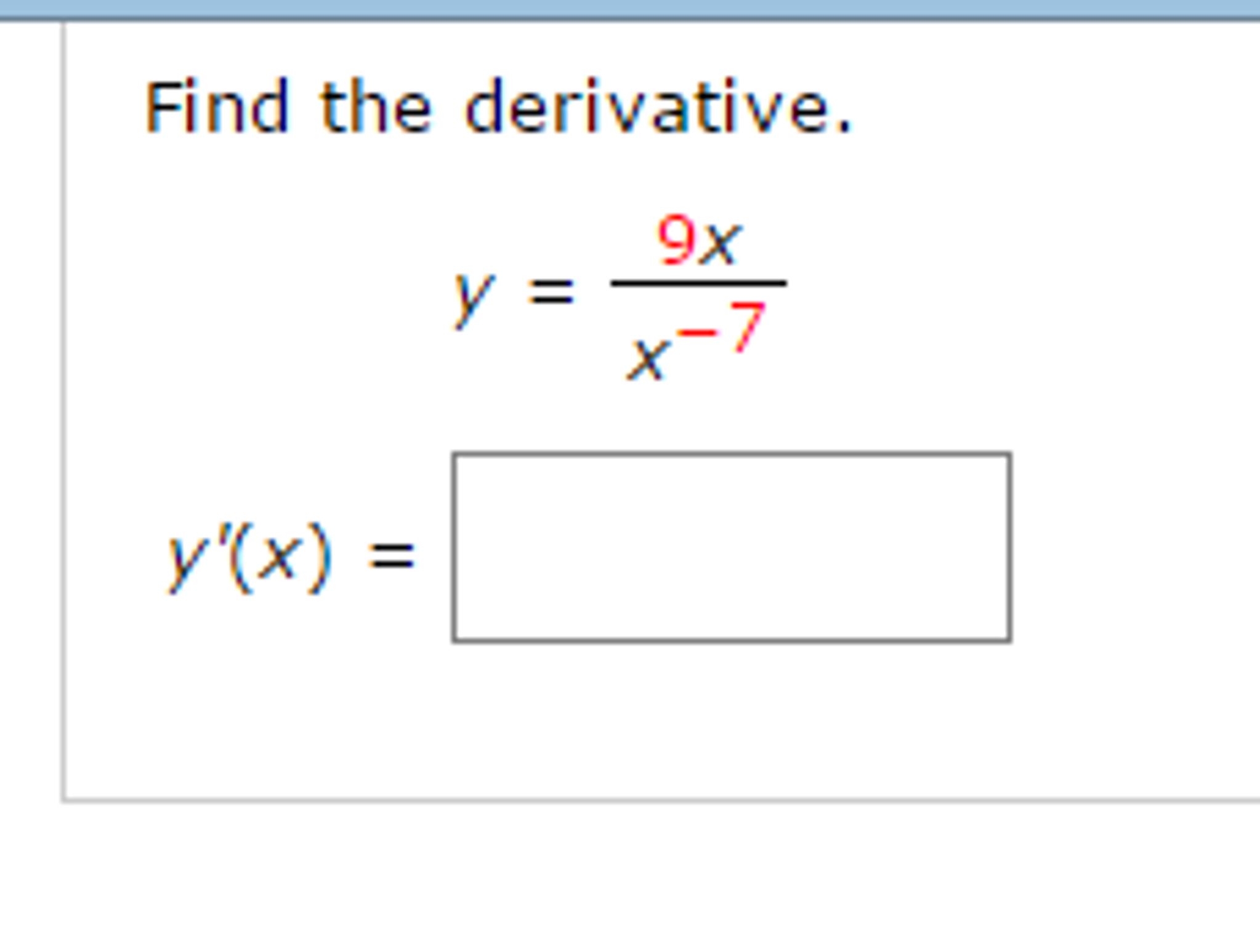



Find The Derivative Y 9x X 7 Y X Find The Chegg Com



Rules Of Differentiation The Constant Multiple Rule




Implicit Differentiation Advanced Example Video Khan Academy




Ac The Derivative Of A Function At A Point




Ac The Derivative Function



Derivatives Of Inverse Functions
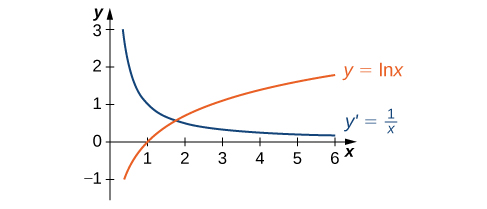



3 9 Derivatives Of Exponential And Logarithmic Functions Calculus Volume 1



Ap Calculus Review Estimating Derivatives From Graphs Magoosh Blog High School




Derivative Of Ln X Video Khan Academy




Common Derivatives Calculus How To
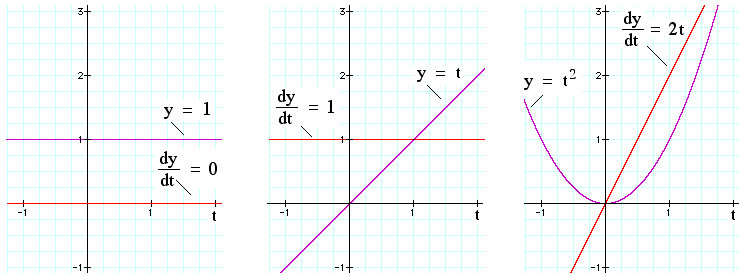



Calculus Differentials And Integrals



Derivative Of Tan X



What Is The Relationship Between The Graph Of A Function And The Graph Of Its Derivative Quora



Assignment 2 Write Up




The Graph Of Y F X The Derivative Of F X Is Shown Below Given F 4 2 Evaluate F 4 Brainly Com



5 Derivative Of The Logarithmic Function
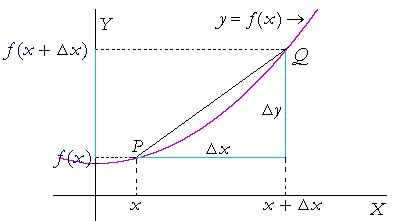



The Meaning Of The Derivative An Approach To Calculus



How To Sketch The Derivative Gra



1



The Derivative



Graph Of Y X X Youtube




Reading The Derivative S Graph Teaching Calculus



Curve Sketching




Implicit Differentiation



5 Derivative Of The Logarithmic Function




Finding The Derivative Of A Function Looking At A Graph Mathematics Stack Exchange
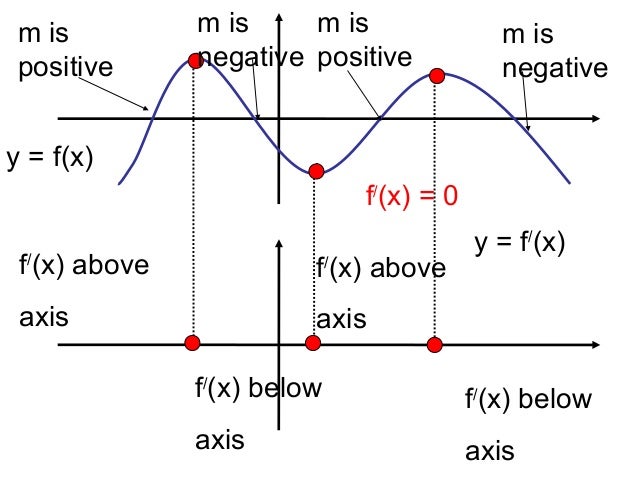



Derivative Graphs




Implicit Differentiation
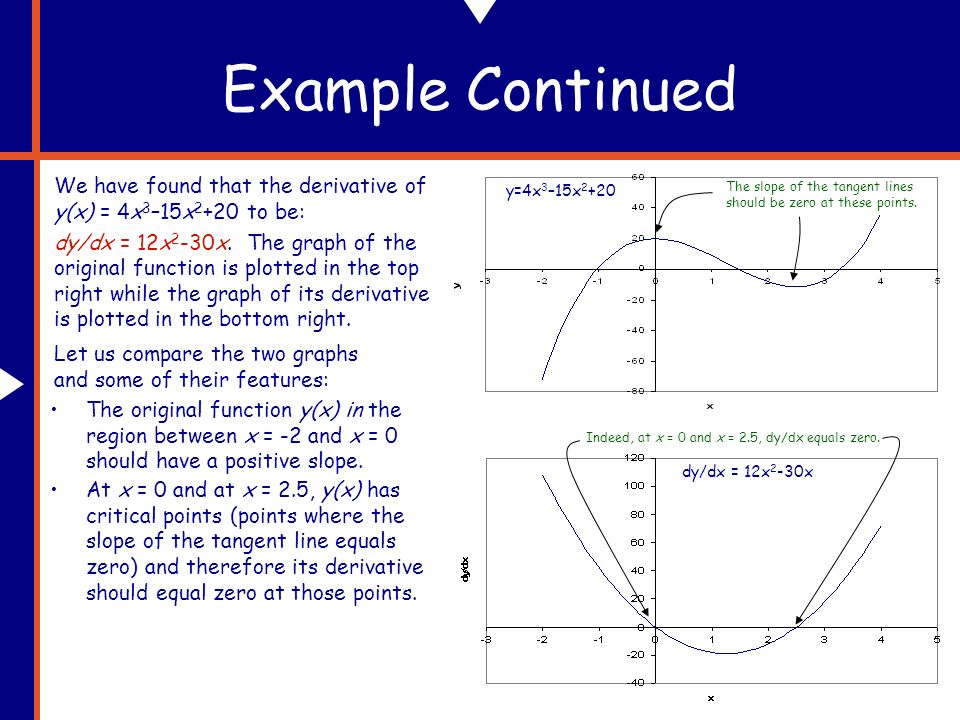



Derivatives A Physics 100 Tutorial Why Do We Need Derivatives In Physics And Life Too Things Are Constantly Changing Specifically What We Ll Be Ppt Download



Differentiation




Derivative Of The F X Y Min X Y Mathematics Stack Exchange
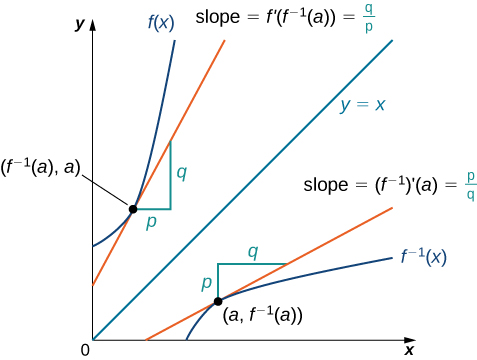



3 7 Derivatives Of Inverse Functions Mathematics Libretexts



Implicit Differentiation



0 件のコメント:
コメントを投稿