THE 30°60°90° TRIANGLE THERE ARE TWO special triangles in trigonometry One is the 30°60°90° triangle The other is the isosceles right triangle They are special because, with simple geometry, we can know the ratios of their sides Theorem In a 30°60°90° triangle the sides are in the ratio 1 2 We will prove that belowWhat is a Triangle?Examples of triangles area of a triangle sum of the angles of a triangle The Pythagorean Theorem

30 60 90 Triangle Rules Sides Ratio Of A 30 60 90 Triangle Video Lesson Transcript Study Com
Theorem 30 60 90 triangle equation
Theorem 30 60 90 triangle equation-The triangle is also a right triangle The Formulas of the Given that X is the shortest side measure, we know we can measure out at the baseline for length X, turn an angle of 60 degrees, and have a new line that eventually intersects the line from the larger side at exactly 30 degrees The formulas for finding the rest of the triangle from just X are the following, where YTriangle What you learned After working your way through this lesson and video, you've learned What a triangle is;



30 60 90 Special Right Triangle Calculator Inch Calculator
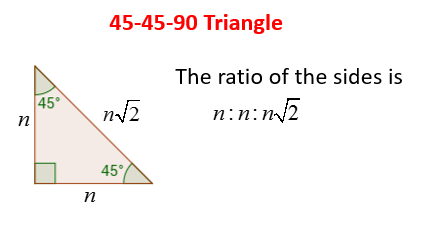
30 60 90 Triangle Theorem Ratio And Formula Video Triangles On Sat Math Geometry Strategies And Practice How To Find The Sides Of A 30 60 90 Right Triangle Math Understanding 30 60 90 Triangles High School Math 30 60 90 Triangles Kates Math Lessons An Appearance Of A 30 60 90 Triangle Find out what are the sides, hypotenuse, area and perimeter of your shape and learn about 45 45 90 triangle formula, ratio and rules If you want to know more about another popular right triangles, check out this 30 60 90 triangle tool and the calculator for special right trianglesA 45 45 90 triangle is a special type of isosceles right triangle where the two legs are congruent to one another and the nonright angles are both equal to 45 degrees Many times, we can use the Pythagorean theorem to find the missing legs or hypotenuse of 45 45 90 triangles The ratio of the sides to the hypotenuse is always 11square root
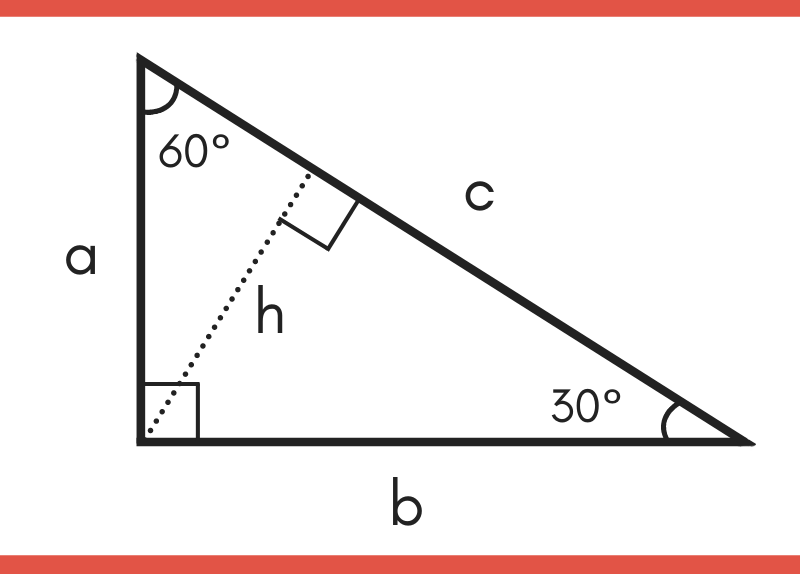
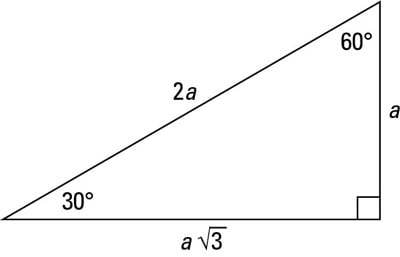
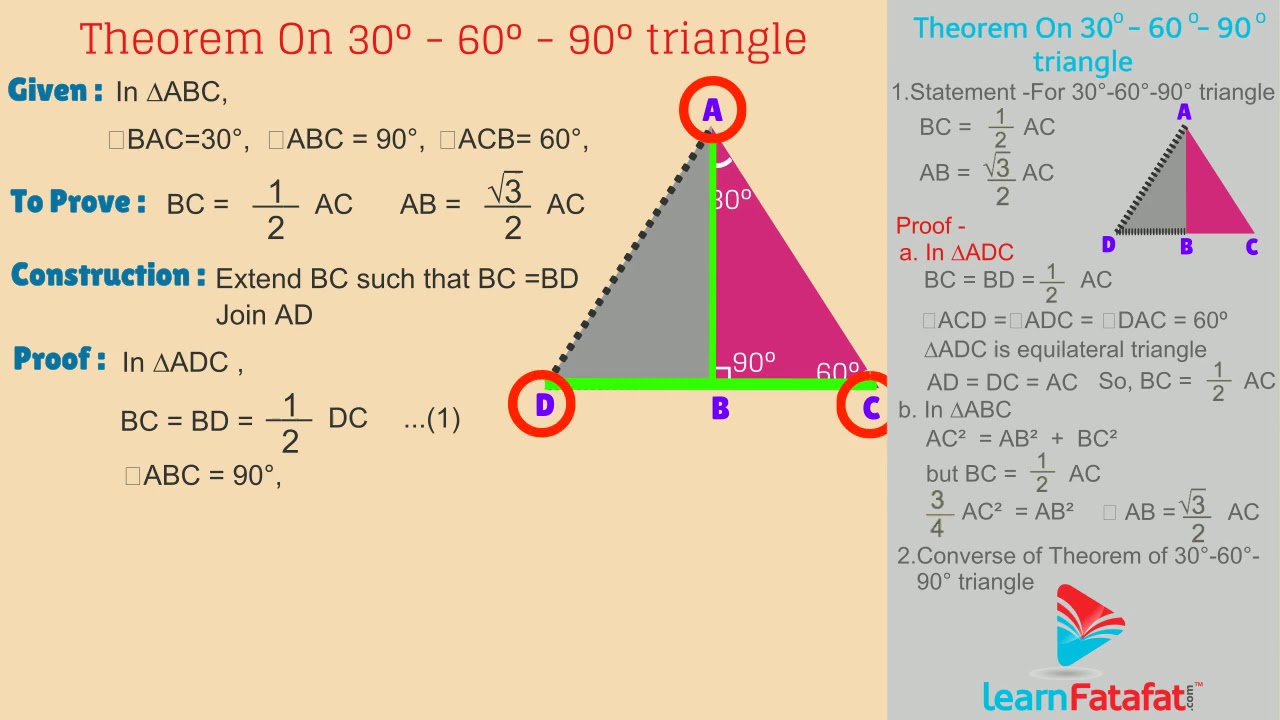
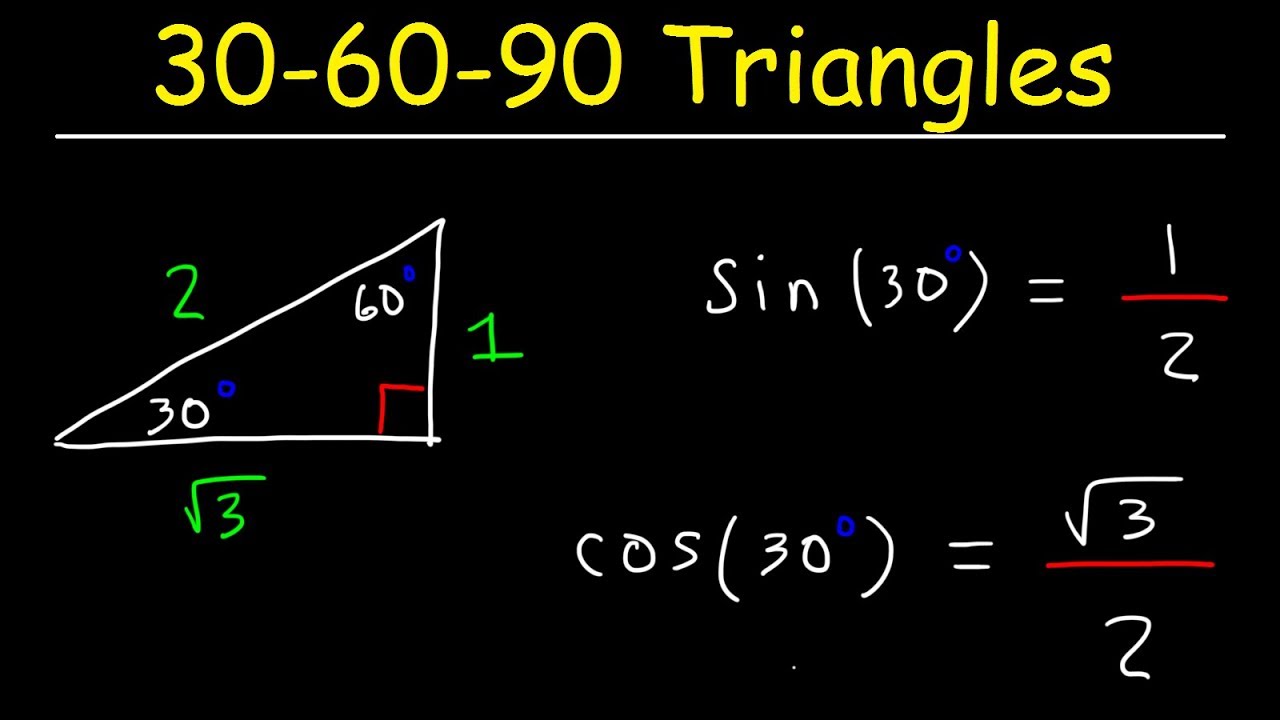
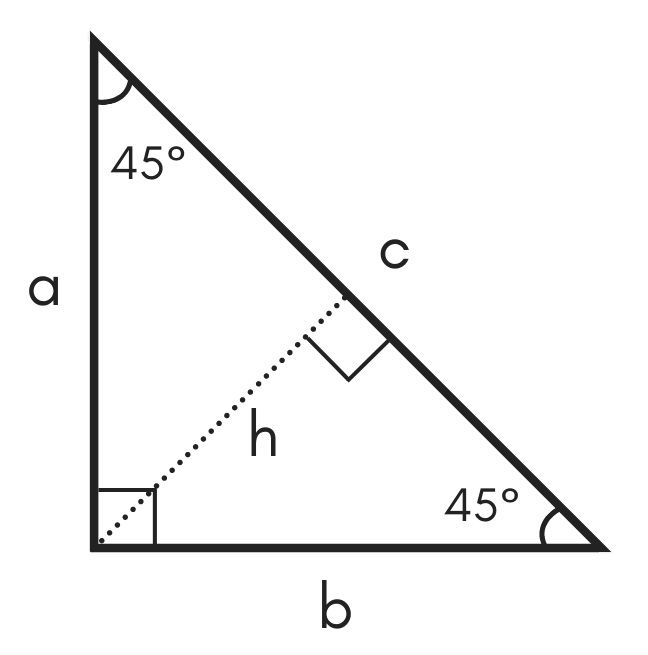
of the hypotenuse of a 30 60 90 triangle to the length of the shorter leg is 2 1 30 60 90 triangle Because all 30 60 90 triangles are similar, the ratio of the length of the longer leg to the length of the shorter leg is always 3 1 This result is summarized in the theorem below 103 30 60 90 Triangles 60 30 1 2 b P P R 6 6 3 6060The two legs of a triangle are always equal The hypotenuse of the triangle is always opposite the right angle There are two formulas for the lengths of the sides of a triangle Then, what is the 30 60 90 triangle formula?Triangletheorempropertiesformula Shared lesson activities for Triangle Theorem, Properties & Formula Go back to all lesson plans
To learn more about Triangles enrol in our full course now https//bitly/Triangles_DMIn this video, we will learn 000 triangle017 proof of 306Triangle (Theorem, Ratio, & Formula) View Course Find a Tutor Next Lesson What is a Triangle? Let's recap the formulas from the Triangle Theorem here in an easytoread form Lesson Summary triangle means a triangle with two 45 degree angles and one 90 degree angle A 45



A Quick Guide To The 30 60 90 Degree Triangle Dummies



1
Another way to use this triangles is to put in the general Pythagorean theorem With this, you can also calculate the values of a side in a triangle given other sides of the same right angle triangle How is triangles solved?A triangle is one of the few special right triangles with angles and side ratios that are consistent and predictable Specifically, every triangle has a 30º angle, a 60º angle, and a 90º angle Since these angles stay the same, the ratio between the length of the sides also remains the sameWatch more videos on http//wwwbrightstormcom/math/geometrySUBSCRIBE FOR All OUR VIDEOS!https//wwwyoutubecom/subscription_center?add_user=brightstorm2VI




45 45 90 Triangle Theorem Rules Formula Video Lesson Transcript Study Com



1
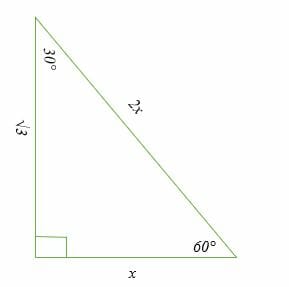
It turns out that in a triangle, you can find the measure of any of the three sides, simply by Draw an equilateral triangle all sides are equal and the angles are all 60 deg From any angle drop a line perpendicular to the base(an altitude) By triangle congruence laws you can prove the 2 resulting triangles are congruent which means the alTriangles Concept A 30 60 90 triangle is a special type of right triangle What is special about 30 60 90 triangles is that the sides of the 30 60 90 triangle always have the same ratio Therefore, if we are given one side we are able to easily find the other sides using the ratio of 12square root of three




30 60 90 Triangle Rules Sides Ratio Of A 30 60 90 Triangle Video Lesson Transcript Study Com



Right Triangle Word Problems Lesson Article Khan Academy
Triangle Research Paper 130 Words1 Page Triangles in that were mostly use in this part of geometry are right triangles There are two theorems that can be uses with the special right triangles, they are triangle theorem and triangle theorem The legs of a are the same In a triangle, the short legA theorem in Geometry is well known The theorem states that, in a right triangle, the side opposite to 30 degree angle is half of the hypotenuse I have a proof that uses construction of equilateral triangle Is the simpler alternative proof possible using school level Geometry I want to give illustration in class roomAnswer (1 of 3) A triangle is special because of the relationship of its sides Hopefully, you remember that the hypotenuse in a right triangle is the longest side, which is also directly across from the 90 degree angle It turns out that in a triangle



30 60 90 Triangles P4 Kate S Math Lessons




Conquering Right Triangles The Pythagorean Theorem On Act Math Part 1 Magoosh Blog High School
The 30–60–90 Day Plan is a document prepared by a job seeker and presented during an interview It is an outline of what the candidate intends or proposes to achieve in the first 90 days, if hired for the role Beside above, what are the sides of a 30 60 90 Triangle?A triangle is a right triangle with angle measures of 30º, 60ºAlthough all right triangles have special features – trigonometric functions and the Pythagorean theorem The most frequently studied right triangles, the special right triangles, are the 30, 60, 90 Triangles followed by the 45, 45, 90 triangles



How To Work With 30 60 90 Degree Triangles Education Is Around
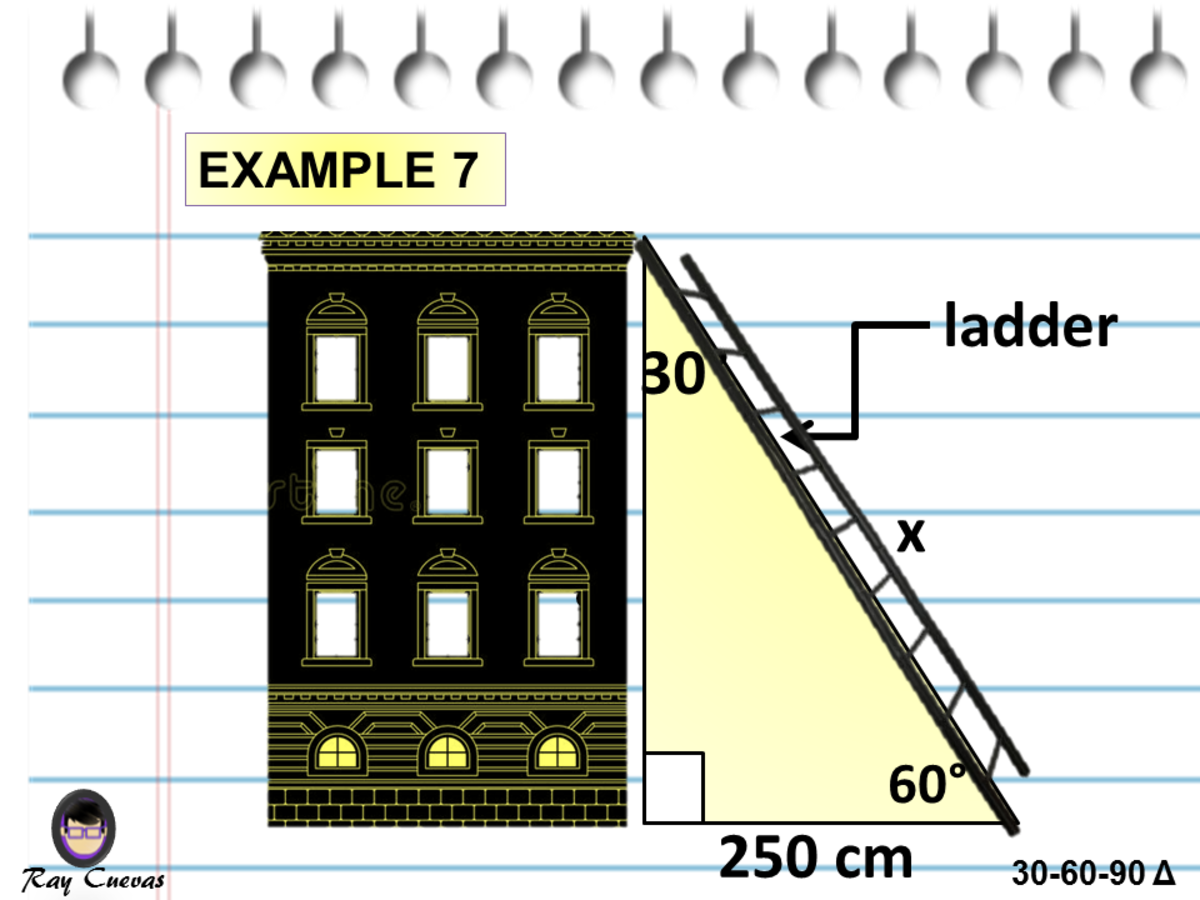



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation
The properties and rules of a triangle;Using the pythagorean theorem – As a right angle triangle, the length of the sides of a 45 45 90Definitions and formulas for the area of a triangle, the sum of the angles of a triangle, the Pythagorean theorem, Pythagorean triples and special triangles (the triangle and the triangle) Just scroll down or click on what you want and I'll scroll down for you!



Identifying The 30 60 90 Triangles




30 60 90 Right Triangles Free Math Help
All degree triangles have sides with the same basic ratio Two of the most common right triangles are and degree triangles If you look at the 30–60–90degree triangle in radians, it translates to the following In any triangle, you see the following The shortest leg is across from the 30degree angle30 60 90 Triangle Theorem images, similar and related articles aggregated throughout the InternetA triangle is a special right triangle whose angles are 30º, 60º, and 90º The triangle is special because its side lengths are always in the ratio of 1 √32 Any triangle of the form can be solved without applying longstep methods such as the Pythagorean Theorem and trigonometric functions



30 60 90 And 45 45 90 Triangle Calculator
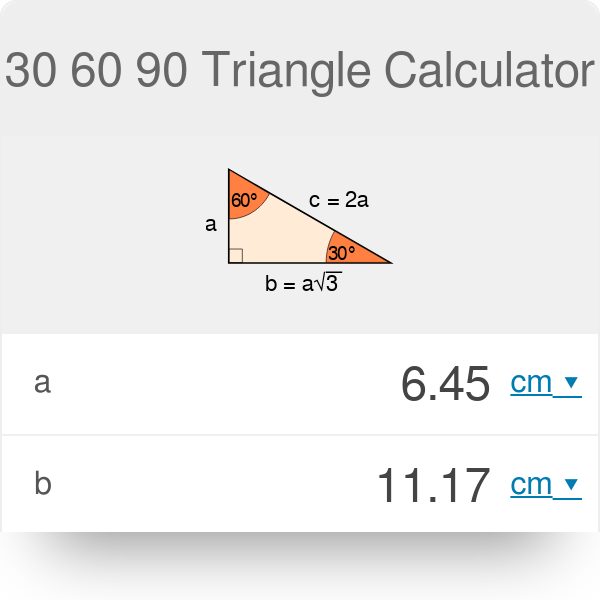



30 60 90 Triangle Calculator Formula Rules
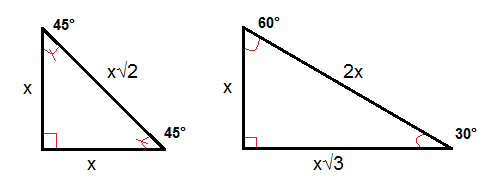
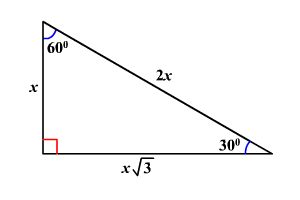
This is also known as the triangle formula for sides yy√32y Let us learn the derivation of this ratio in the triangle proof section Consider some of the examples of a degree triangle with these side lengths Here, in the triangle DEF ∠ F = 30°, ∠ D = 60°, and ∠ E = 90° The side opposite to the 30° angle, DE = y = 2;Solving any mathematical problem related to triangles can be easy if you understand the basics and you know how toTriangle formula and how to solve for the hypotenuse;
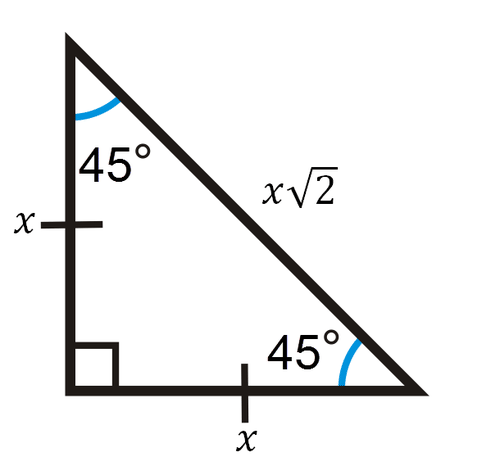



Special Right Triangles Ck 12 Foundation




30 60 90 Triangle Theorem Ratio Formula Video
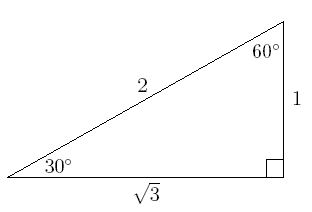
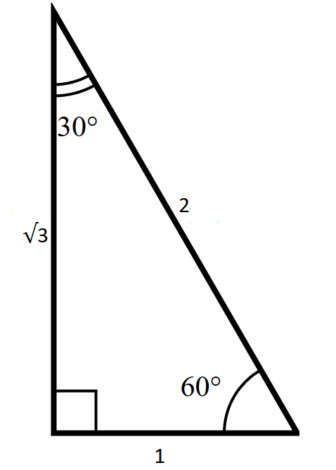
A triangle is a special right triangle whose angles are 30º, 60º, and 90º The triangle is special because its side lengths are always in the ratio of 1 √32 What is the formula for a 45 45 90 Triangle?Then ABD is a 30°–60°–90° triangle with hypotenuse of length 2, and base BD of length 1 The fact that the remaining leg AD has length √ 3 follows immediately from the Pythagorean theorem The 30°–60°–90° triangle is the only right triangle whose angles are in an arithmetic progressionA triangle is a right triangle where the three interior angles measure 30 °, 60 °, and 90 ° Right triangles with interior angles are known as special right triangles Special triangles in geometry because of the powerful relationships that unfold
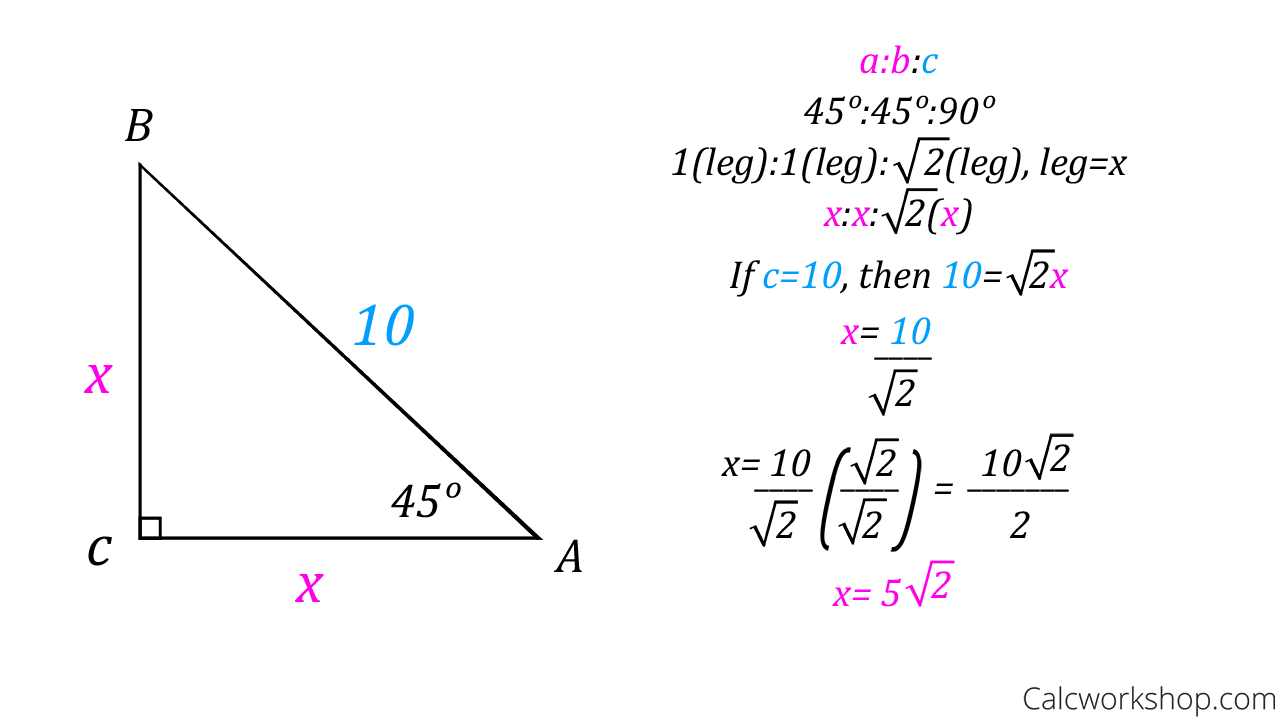



Special Right Triangles Fully Explained W 19 Examples



How To Use The Special Right Triangle 30 60 90 Studypug
Because a right triangle has to have one 90° angle by definition and the other two angles must add up to 90° So $90/2 = 45$) Triangles A triangle is a special right triangle defined by its angles It is a right triangle due to its 90° angle, and the other two angles must be 30° and 60° 345, and RightInstructor Malcolm M Malcolm has a Master's Degree in education and holds four teaching30 60 90 triangle theorem formula Although all right triangles have special features trigonometric functions and the pythagorean theorem According to the 30 60 90 triangle theorem the longer leg is the square root of three times as long as the shorter leg If the shortest side of a 30 60 90 triangle is 5sqrt 3 units long find the length of the side that is opposite the 60




30 60 90 Right Triangles Read Geometry Ck 12 Foundation



30 60 90 Right Triangles Examples Geometry Concepts Youtube
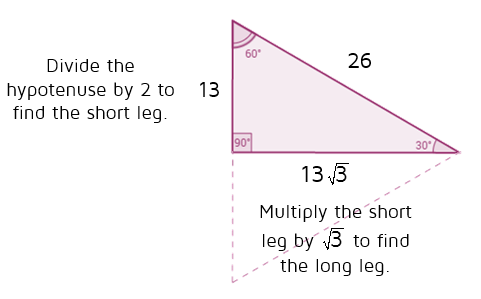
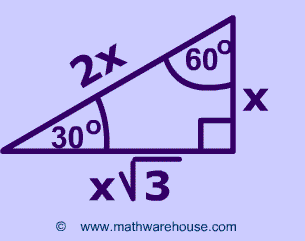
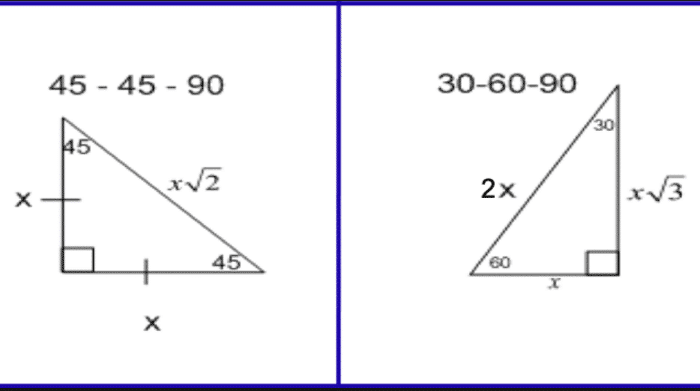
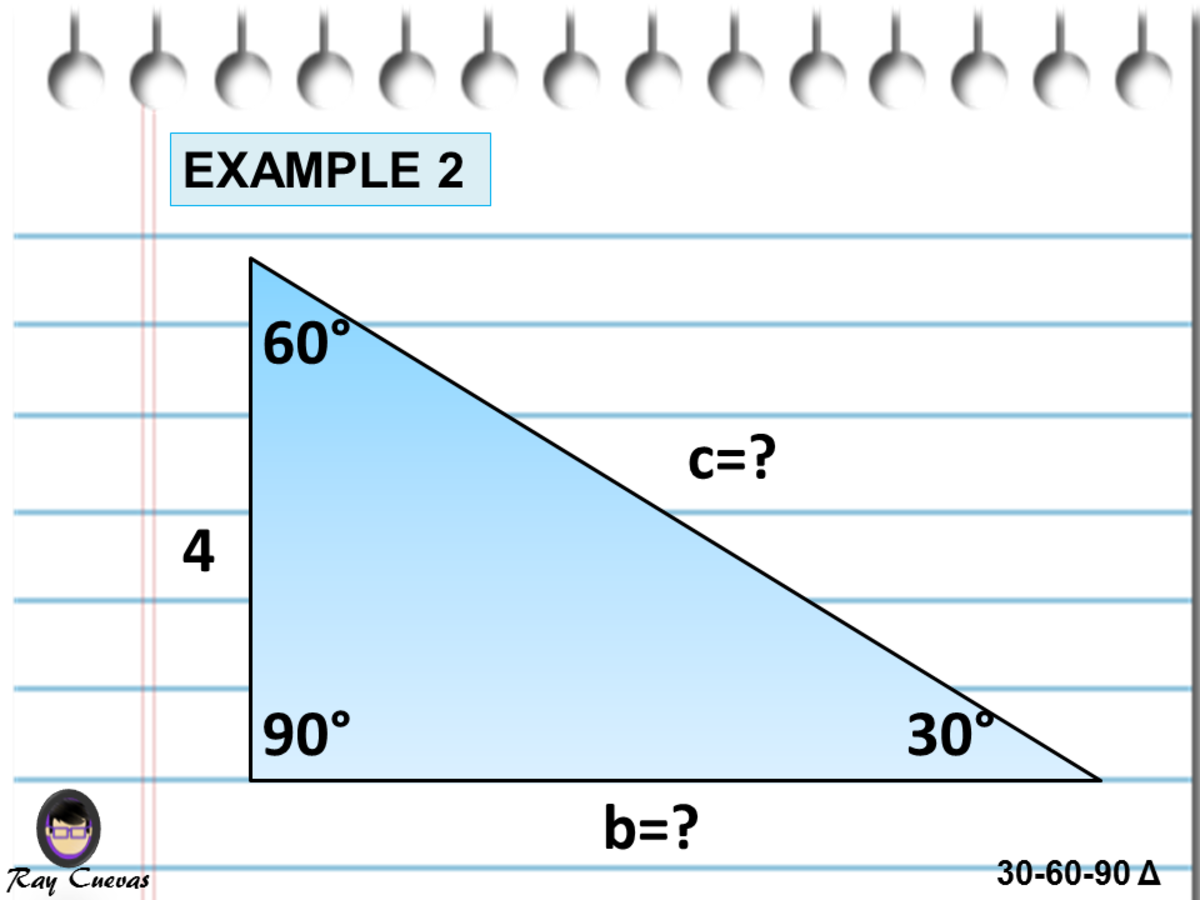
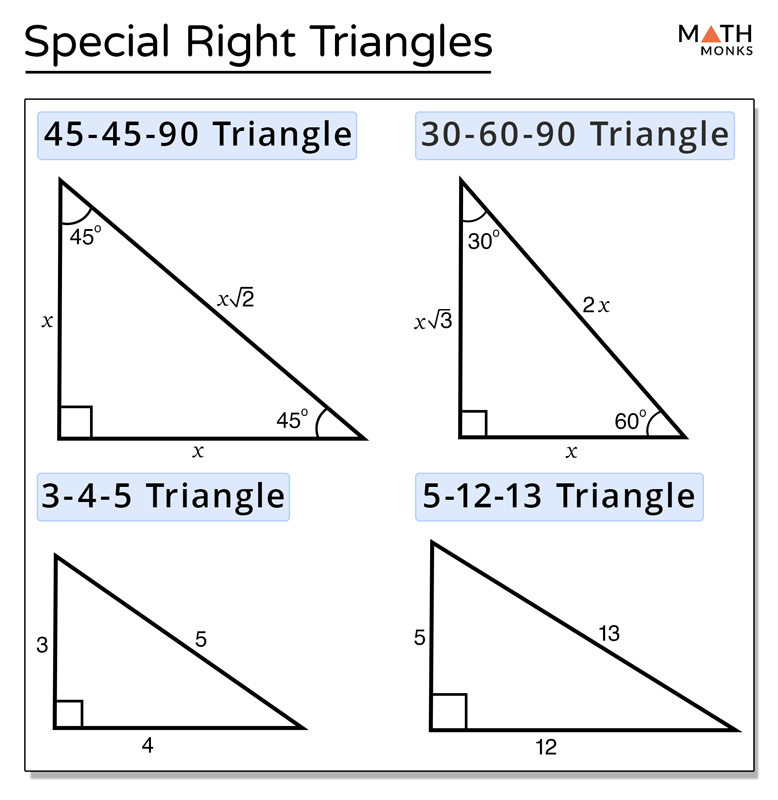
30 60 90 triangle sides If we know the shorter leg length a, we can find out that b = a√3 c = 2a If the longer leg length b is the one parameter given, then a = b√3/3 c = 2b√3/3 For hypotenuse c known, the legs formulas look as follows a = c/230 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com The Easy Guide To The 30 60 90 Triangle How To Find The Length Of The Hypotenuse Of A Right Triangle Pythagorean Theorem Sat Math Special Right Triangle Wikipedia What Is The Area Of A 30 60 And 90 Triangle If The Hypotenuse Is 12 In Quora Special Right Triangles Video LessonsExample of 30 – 60 90 rule Example 1 Find the missing side of the given triangle As it is a right triangle in which the hypotenuse is the double of one of the sides of the triangle Thus, it is called a triangle where smaller angle will be 30 The longer side is always opposite to 60° and the missing side measures 3√3 units in




Special Right Triangles 30 60 90 And 45 45 90 Triangles Youtube



The Easy Guide To The 30 60 90 Triangle
Right triangles are one particular group of triangles and one specific kind of right triangle is a right triangle As the name suggests, the three angles in the triangle are 30, 60, andThe side opposite to theSee also Side /angle relationships of a triangle In the figure above, as you drag the vertices of the triangle to resize it, the angles remain fixed and the sides remain in this ratio Corollary If any triangle has its sides in the ratio 1 2 √3, then it is a triangle



30 60 90 Triangle Math Right Triangles Showme



Special Right Triangles Formulas 30 60 90 And 45 45 90 Special Right Triangles Examples Pictures And Practice Problems
Shared lesson activities for Triangle Theorem, Properties & Formula ALevel Maths 17 B612 Polynomials Solving Problems and Extending the Factor Theorem This video is designed for the new specification for ALevel Maths, first teaching in September 17 The sides of a right triangle lie in the ratio 1√32 The side lengths and angle measurements of a right triangle Credit Public Domain We can see why these relations should hold by plugging in the above values into the Pythagorean theorem a2 b2 = c2 a2 ( a √3) 2 = (2 a) 2 a2 3 a2 = 4 a2The 45°45°90° triangle, also referred to as an isosceles right triangle, since it has two sides of equal lengths, is a right triangle in which the sides corresponding to the angles, 45°45°90°, follow a ratio of 11√ 2 Like the 30°60°90° triangle, knowing one side length allows you to determine the lengths of the other sides of a 45°45°90° triangle




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com
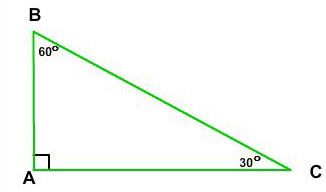



30 60 90 Right Triangle Side Ratios Expii
Right triangle calculator, 30 60 90 formula, 45 triangle, special area, unit circle calculator For example, we can use the triangle formula to fill in all the remaining information blanks of the triangles below Example 1 We can see that this is a right triangle in which the hypotenuse is twice the length of one of the legs This means this must be a triangle and the smaller given side is opposite the 30° The longer leg must, therefore, be opposite the 60The triangle is a special right triangle, as it has a special relationship between its sides If we know the measure of at least one side of the triangle, the special proportions of sides of the triangle could be used to determine the measure of other sides of the same triangle




45 45 90 Triangle Calculator Formula Rules
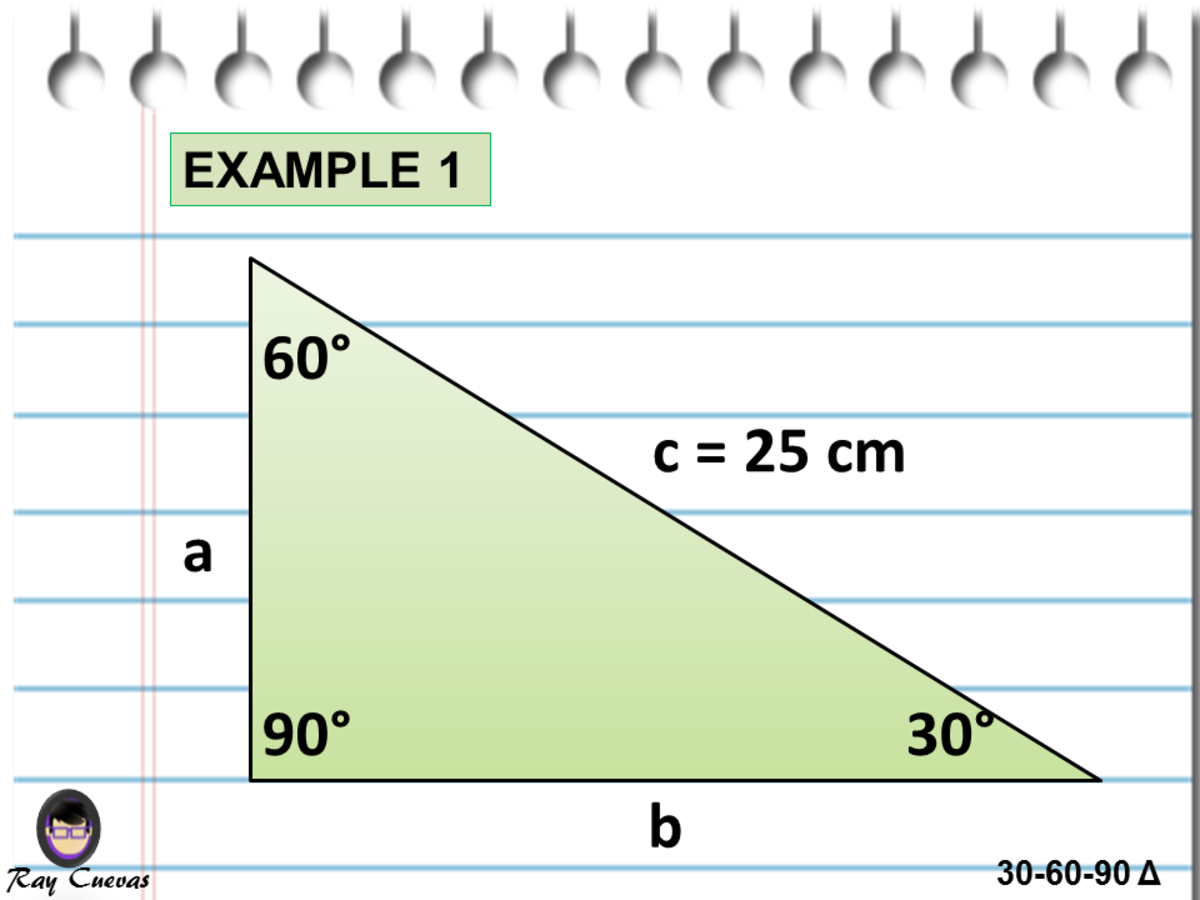



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation
Similarity in Right Angled Triangles 30 60 90 and 45 45 90 Theorem Circle Theorem of External Division of Chords Theorem of Internal Division of Chords Converse of Theorem of the Angle Between Tangent and Secant Theorem of Angle Between Tangent and Secant Converse If a pair of opposite angles of a quadrilateral is supplementary
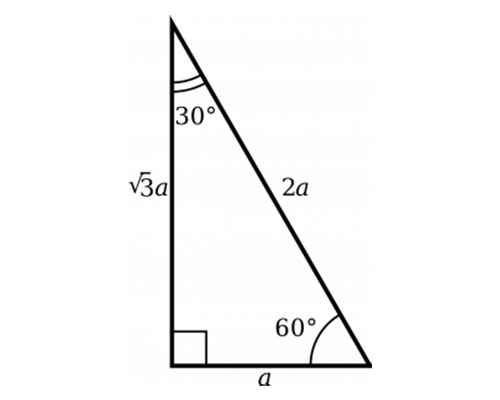



30 60 90 Triangle Sides Examples Angles Full Lesson
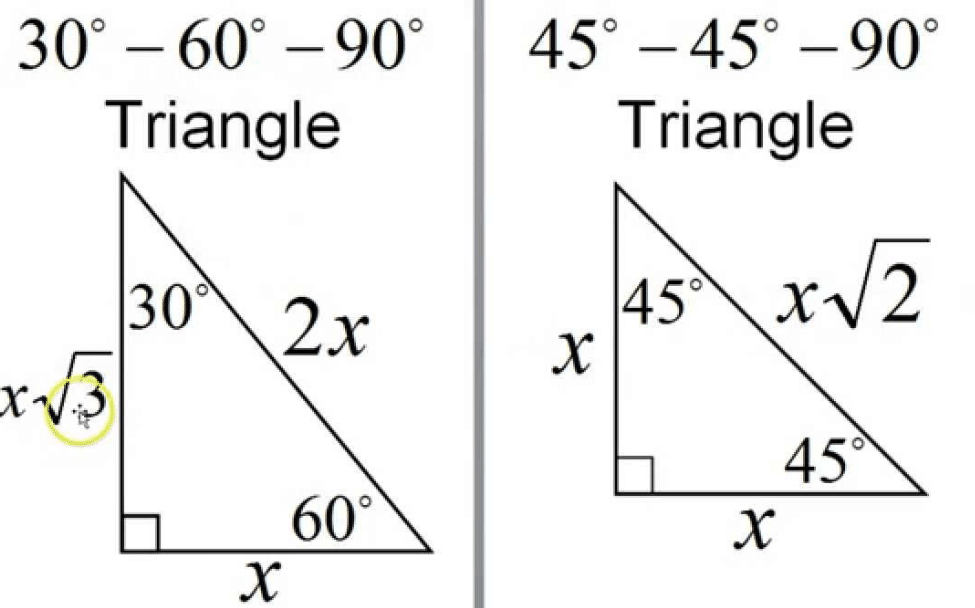



How To Work With 30 60 90 Degree Triangles Education Is Around



The Complete Guide To The 30 60 90 Triangle



30 60 90 Triangle Explanation Examples



Pythagoras Theorem On 30 60 90 Triangle Youtube




30 60 90 Special Right Triangle Calculator Inch Calculator
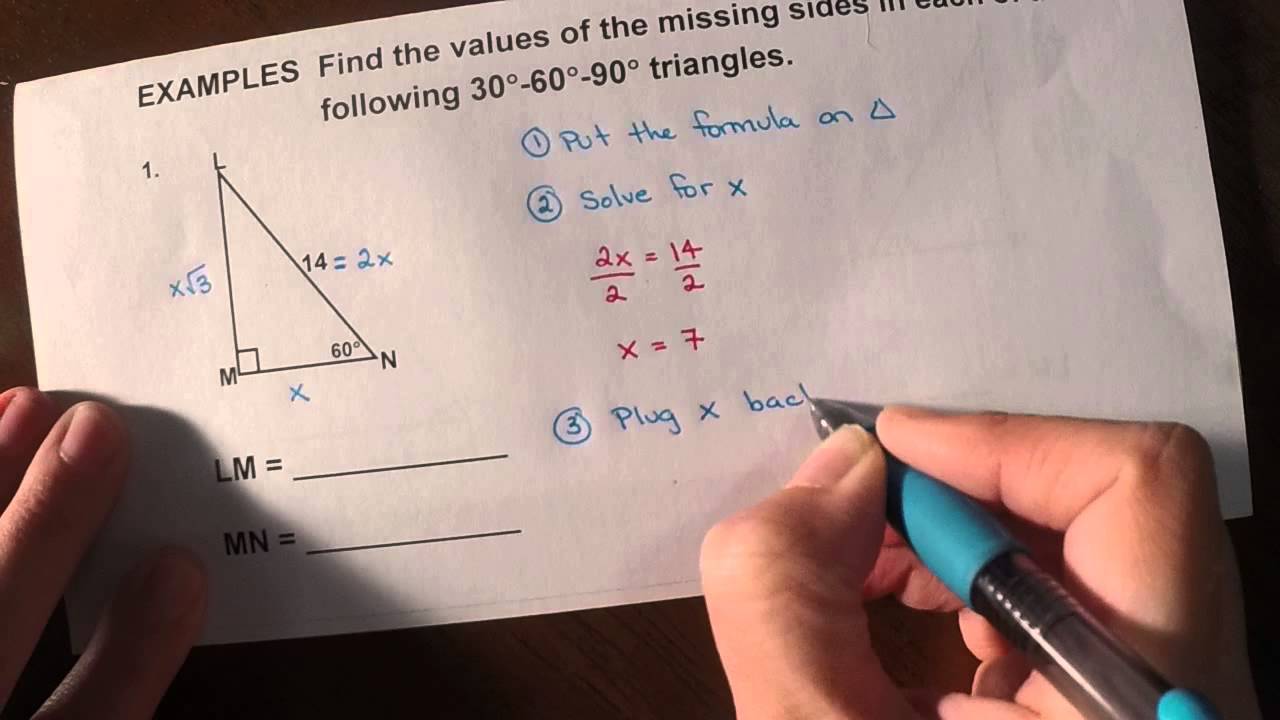



30 60 90 Triangles Youtube




30 60 90 Triangle Theorem Ratio Formula Video
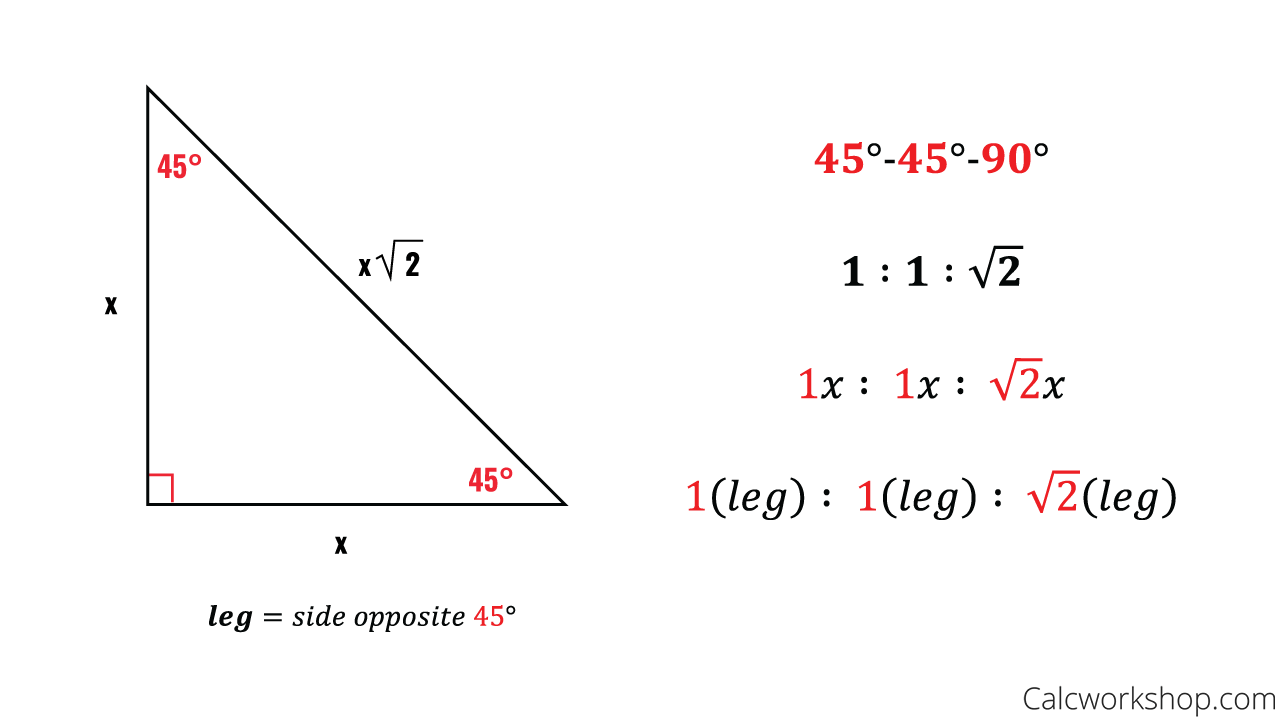



Special Right Triangles Fully Explained W 19 Examples
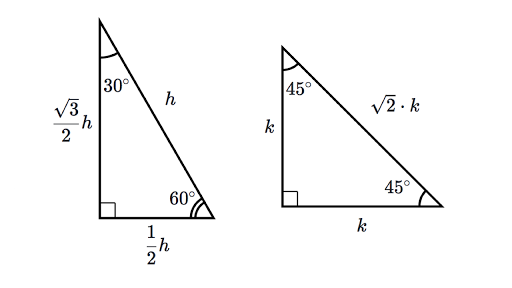



Special Right Triangles Review Article Khan Academy



The Easy Guide To The 30 60 90 Triangle




Solved Deriving The Ratio Of The Sides Of A 30 60 90 Chegg Com



Right Triangles Gmat Free
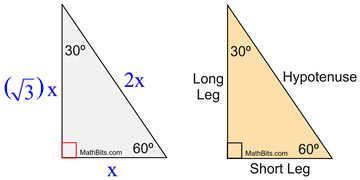



Special Right Triangle 30 60 90 Mathbitsnotebook Geo Ccss Math



The Length Of The Hypotenuse Of A 30 60 90 Triangle Is 12cm What Is The Length Of The Longer Leg What Is The Length Of The Shorter Leg Quora



The Easy Guide To The 30 60 90 Triangle
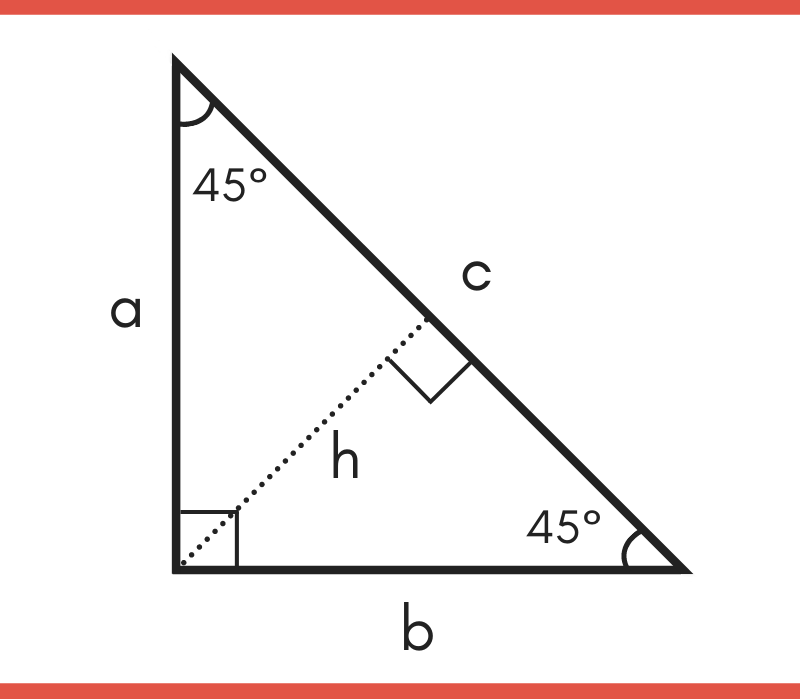



45 45 90 Special Right Triangle Calculator Inch Calculator
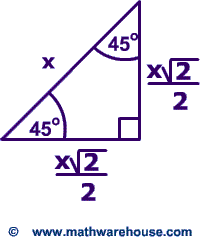



Special Right Triangles Formulas 30 60 90 And 45 45 90 Special Right Triangles Examples Pictures And Practice Problems
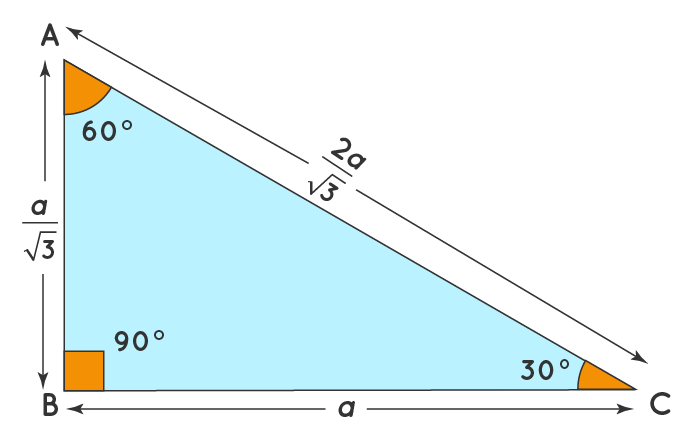



30 60 90 Triangle Definition Theorem Formula Examples




Special Right Triangles Interactive Notebook Page Math Methods Teaching Geometry Teaching Math
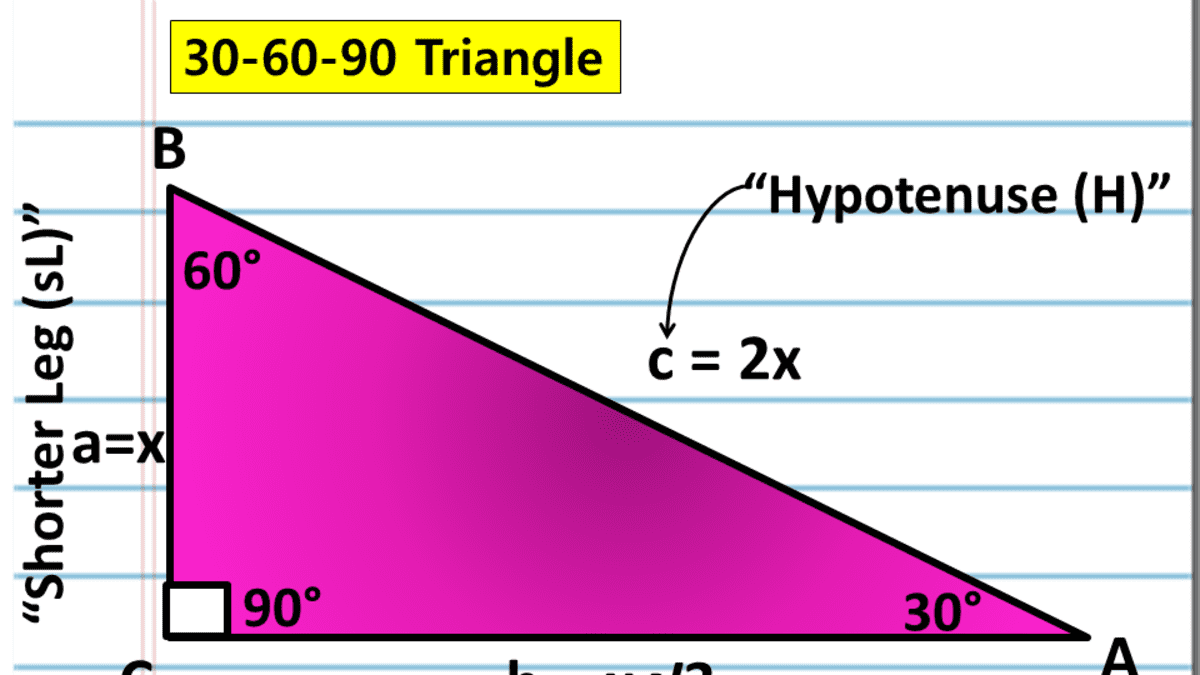



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




30 60 90 Triangles




Foundation Class X Theorem Of 30 60 90 Triangle In Marathi Offered By Unacademy




30 60 90 Triangle Explanation Examples



5 5 Special Triangles




Math Example Right Triangles Example 24 Media4math




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com
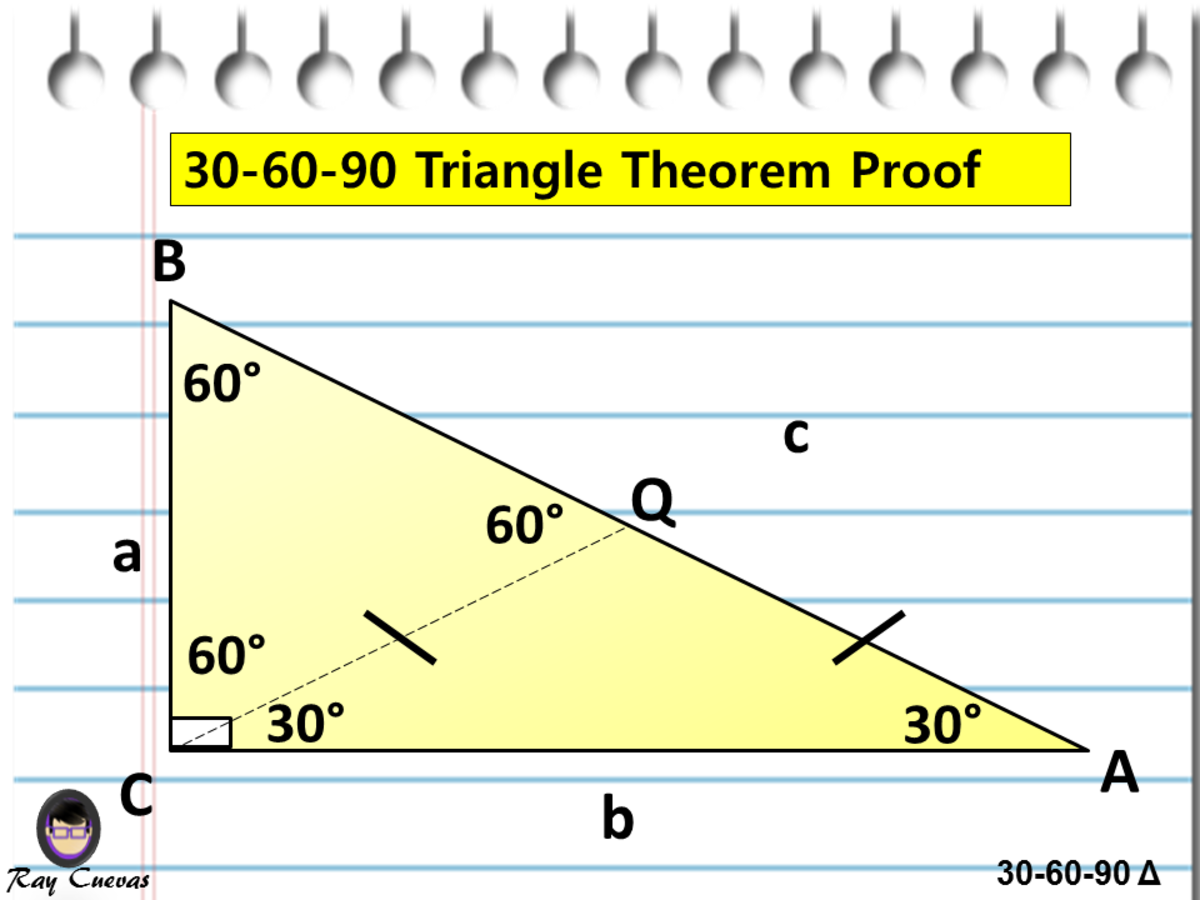



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation



Special Right Triangles




30 60 90 Triangle Theorem Ratio Formula Video



30 60 90 Triangles Special Right Triangle Trigonometry Youtube



Special Right Triangles Complete Reference Guide The Education



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation



45 45 90 And 30 60 90 Triangles Zona Land Education



Special Right Triangles Definition Formula Examples
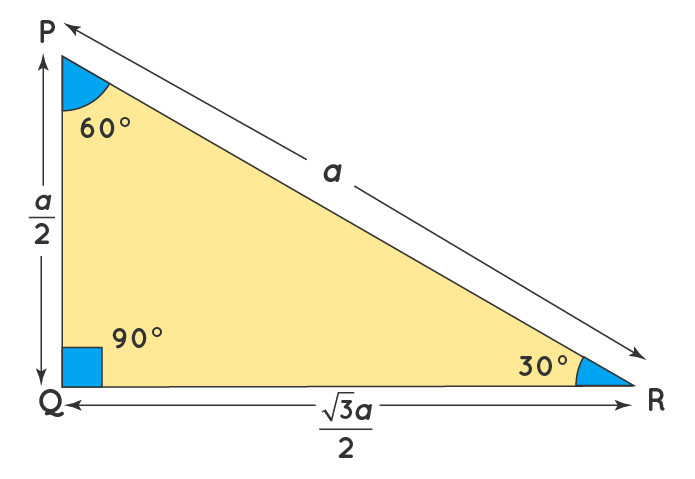



30 60 90 Triangle Definition Theorem Formula Examples
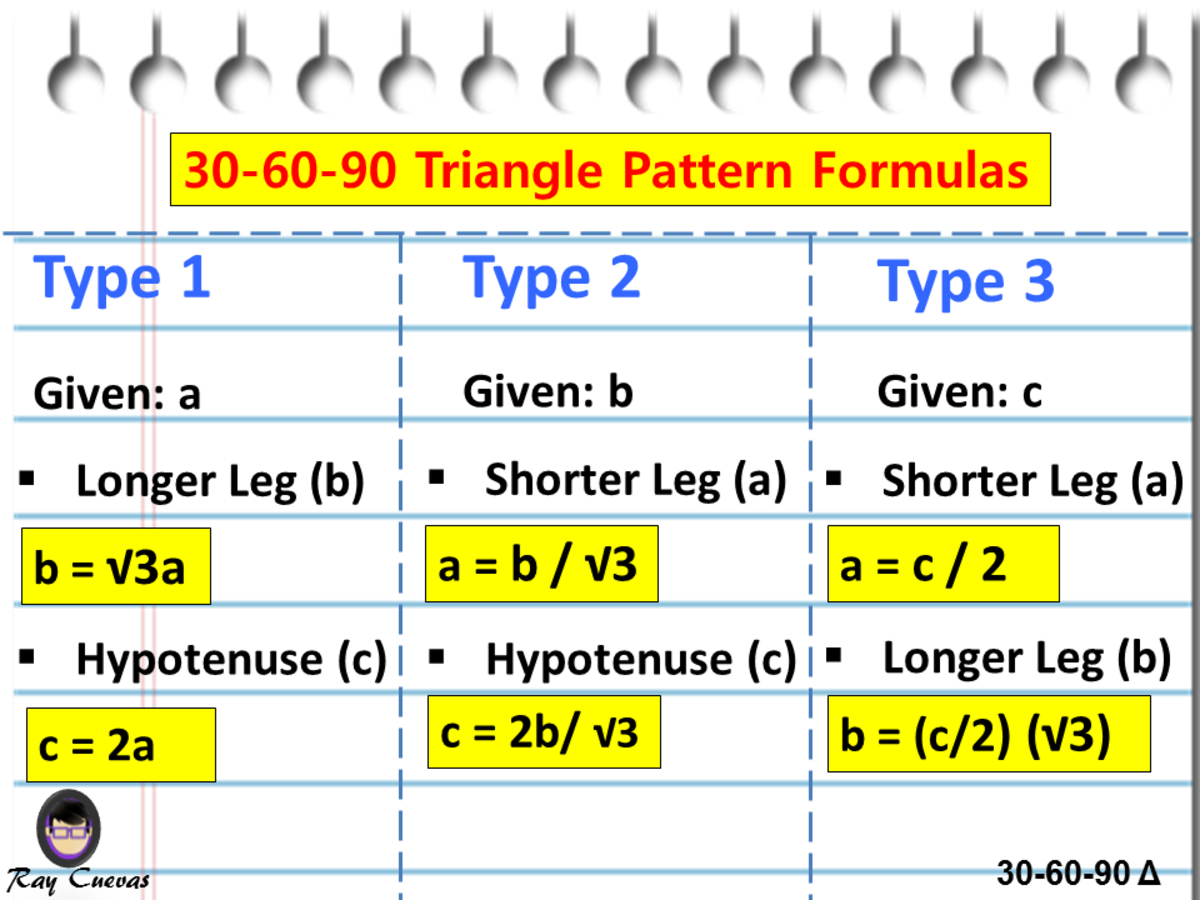



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation
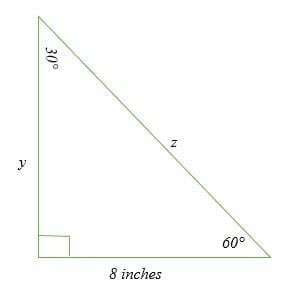



30 60 90 Triangle Explanation Examples
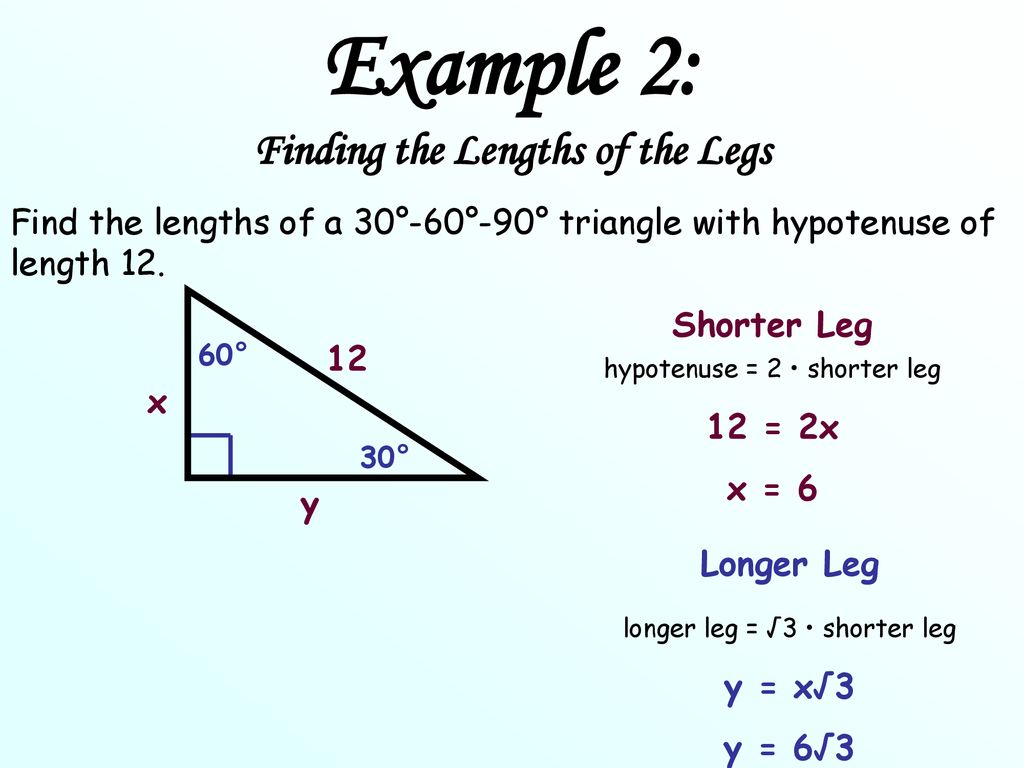



Objective To Use The Properties Of 30 60 90 Triangle Ppt Download



45 45 90 Special Right Triangle Calculator Inch Calculator



The Converse Of The Pythagorean Theorem And Special Triangles Geometry Right Triangles And Trigonometry Mathplanet



30 60 90 Triangle Formulas Rules And Sides Science Trends



30 60 90 Triangles
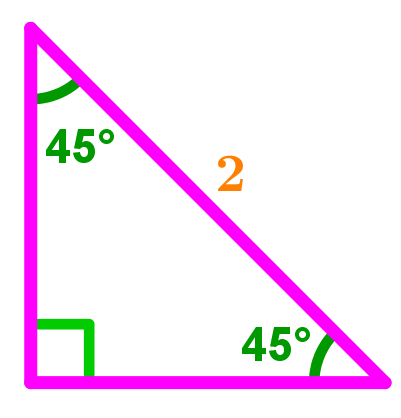



How To Use The Special Right Triangle 45 45 90 Studypug
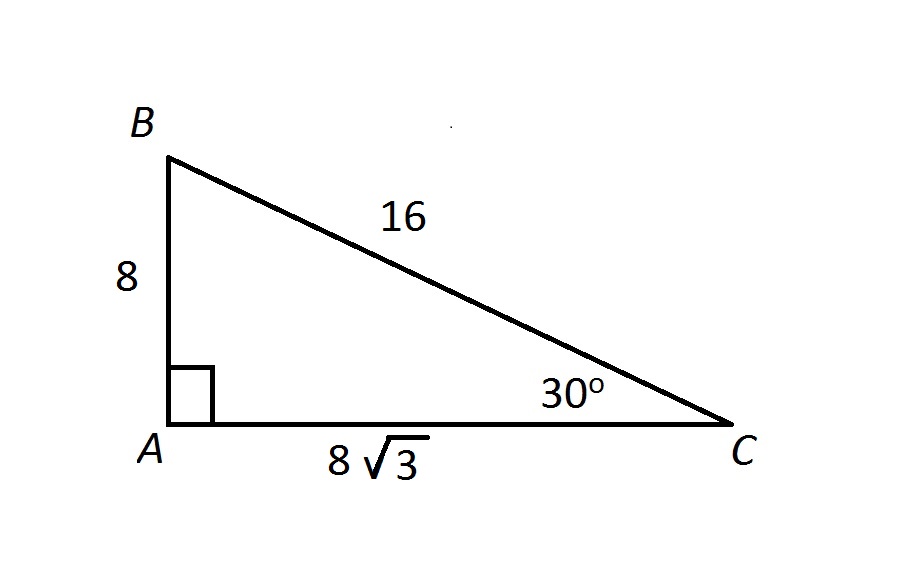



Special Triangles Hiset Math




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com
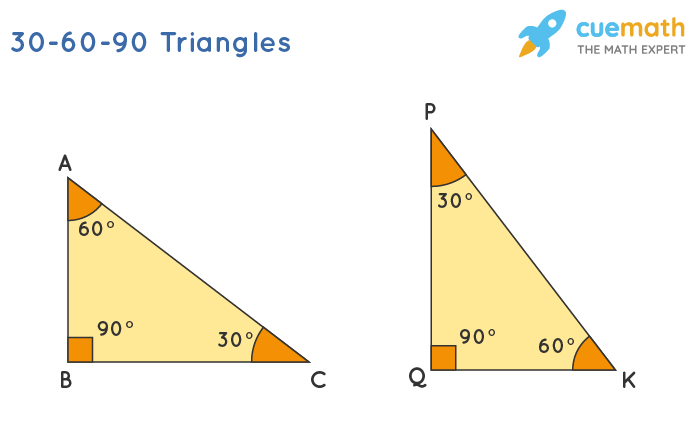



30 60 90 Triangle Definition Theorem Formula Examples
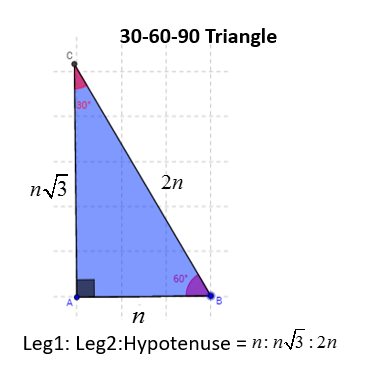



30 60 90 Right Triangles Solutions Examples Videos
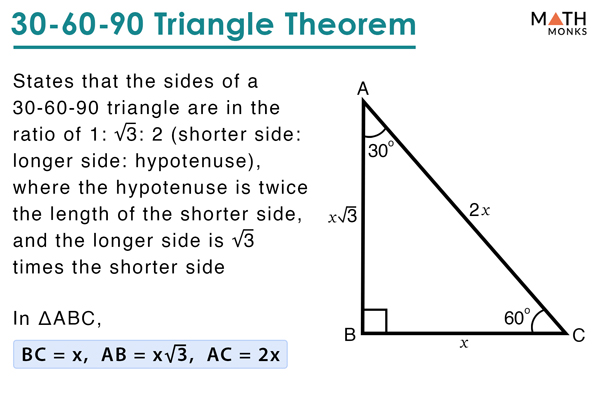



30 60 90 Triangle Definition Formulas Examples
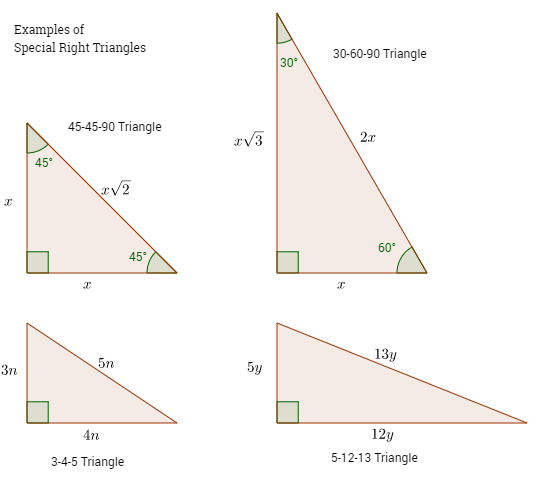



Special Right Triangles Video Lessons Examples And Solutions
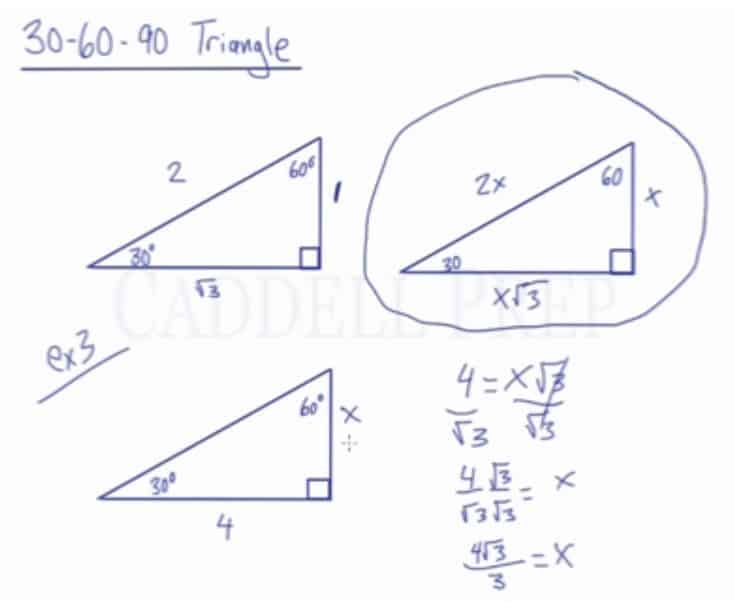



Learn About The 30 60 90 Triangle Caddell Prep Online
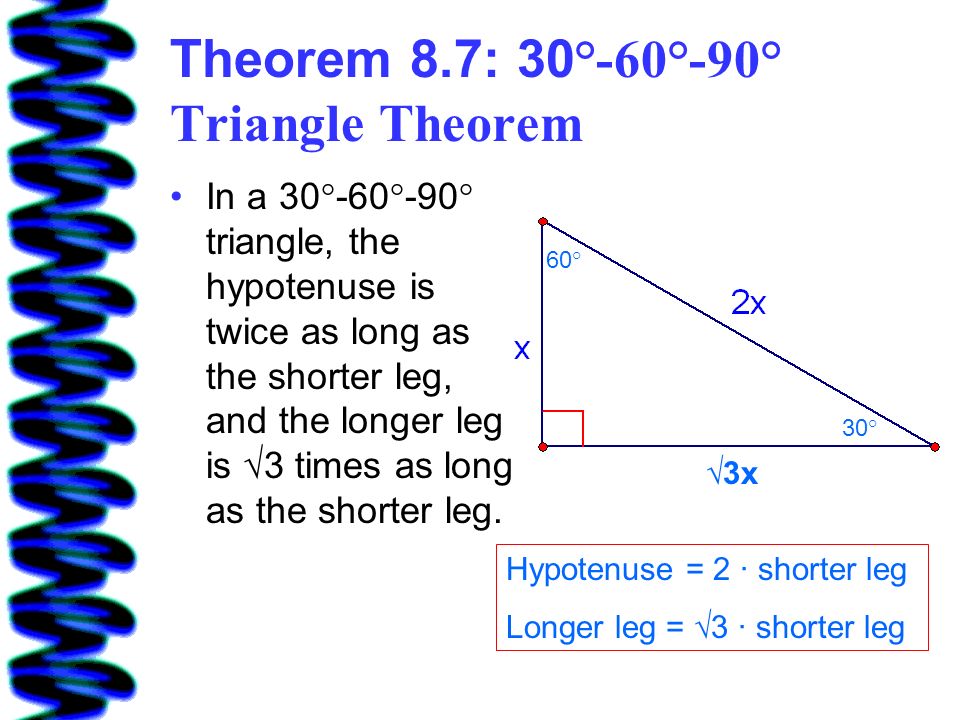



8 2 Special Right Triangles Ppt Video Online Download
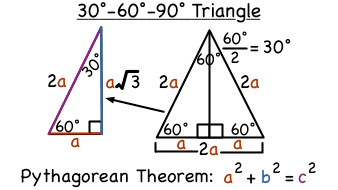



What Is A 30 60 90 Degree Triangle Virtual Nerd



Solve A 30 60 90 Triangle With Gradea




30 60 90 Triangle Theorem Proof Don T Memorise Youtube
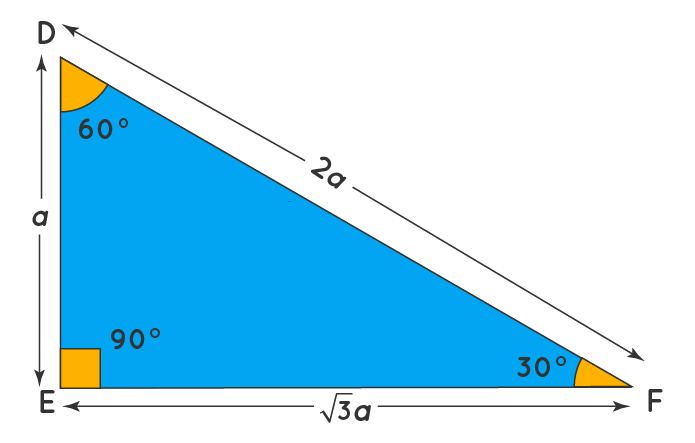



30 60 90 Triangle Definition Theorem Formula Examples




30 60 90 Triangle Calculator Formula Rules
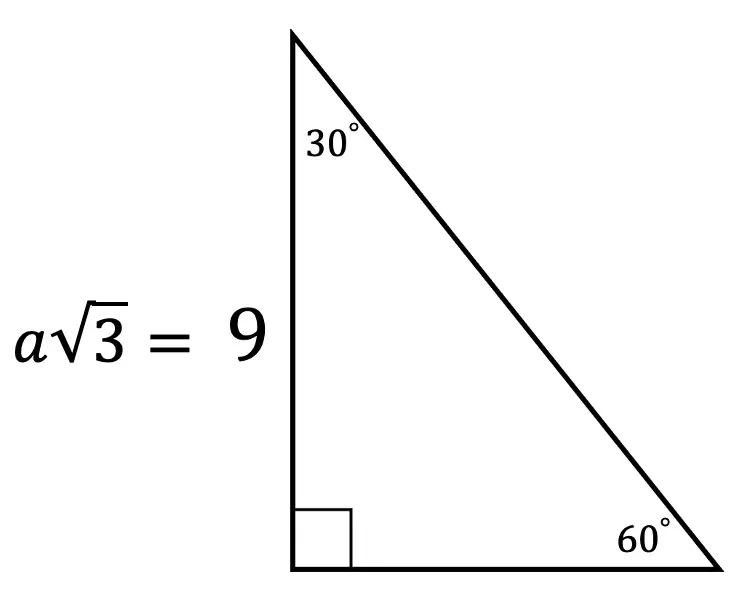



30 60 90 Special Triangles Geometry Mathsux 2




30 60 90 Triangle Theorem Ratio Formula Video



1




30 60 90 Triangle Theorem Ratio Formula Video
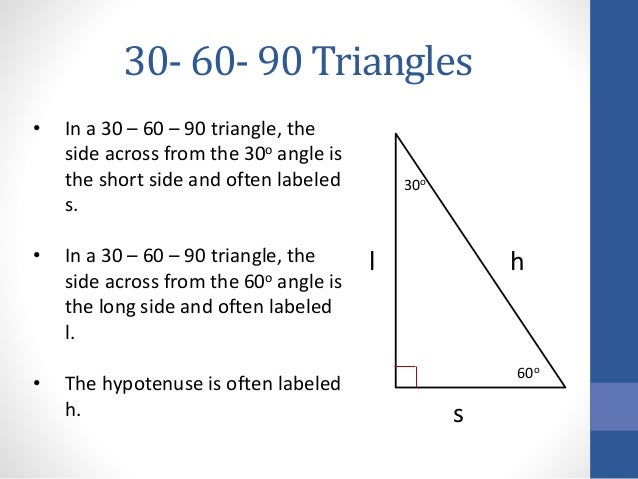



30 60 90 Triangles
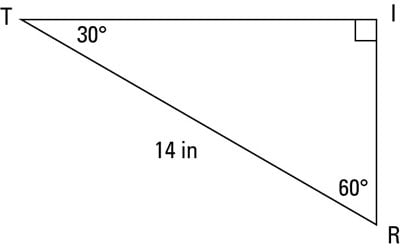



A Quick Guide To The 30 60 90 Degree Triangle Dummies




30 60 90 Triangle Theorem Ratio Formula Video




Special Right Triangles Fully Explained W 19 Examples
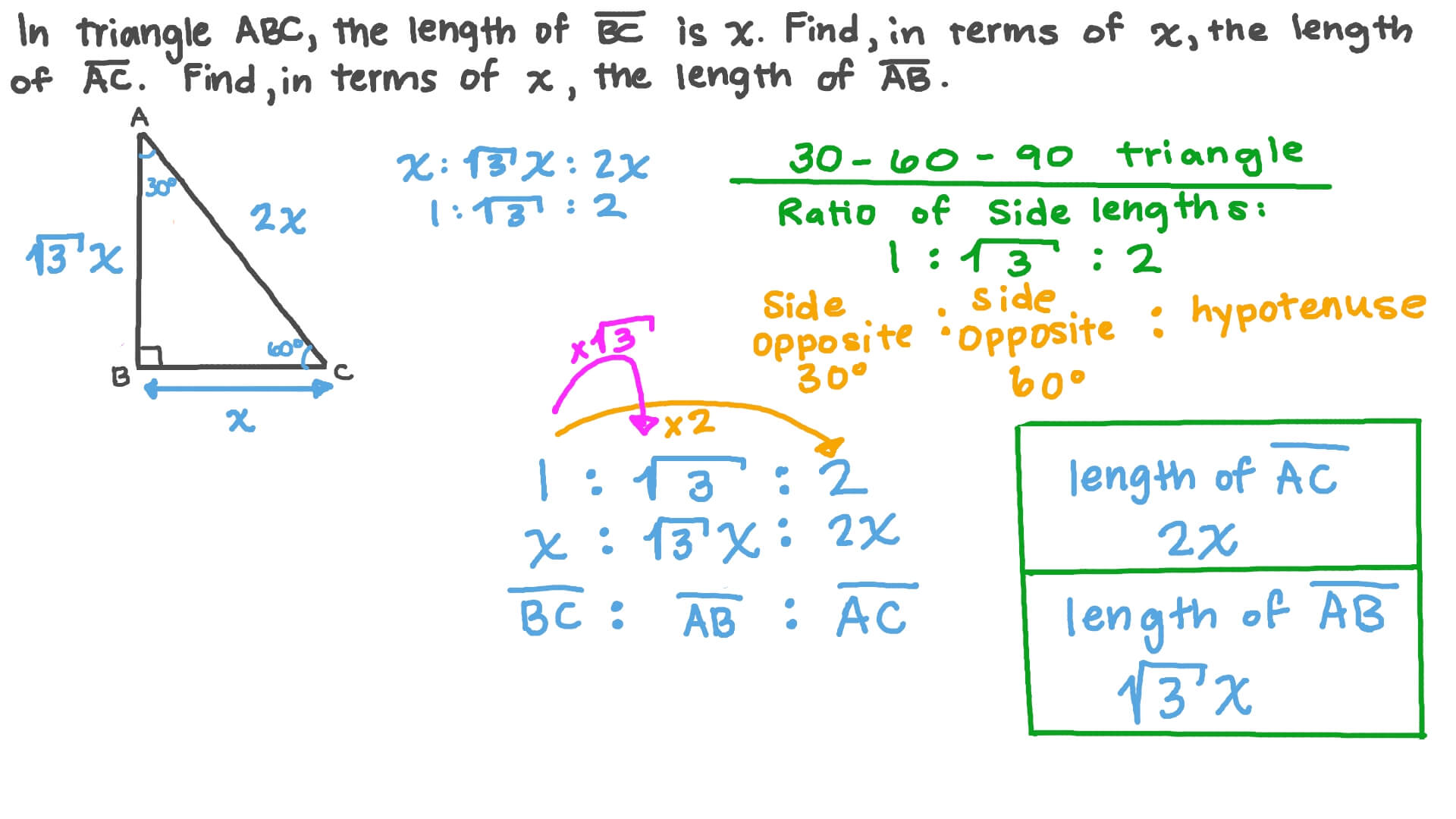



Question Video The Side Lengths Of 30 60 90 Triangles Nagwa




30 60 90 Triangle Theorem Ratio Formula Video
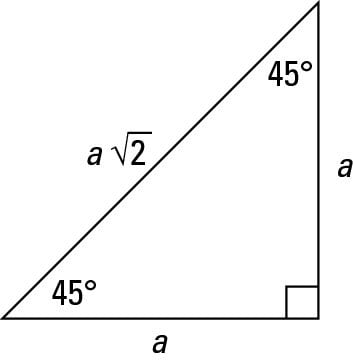



How To Work With 30 60 90 And 45 45 90 Degree Triangles Dummies




Finding The Missing Side Of 30 60 90 Triangle Youtube
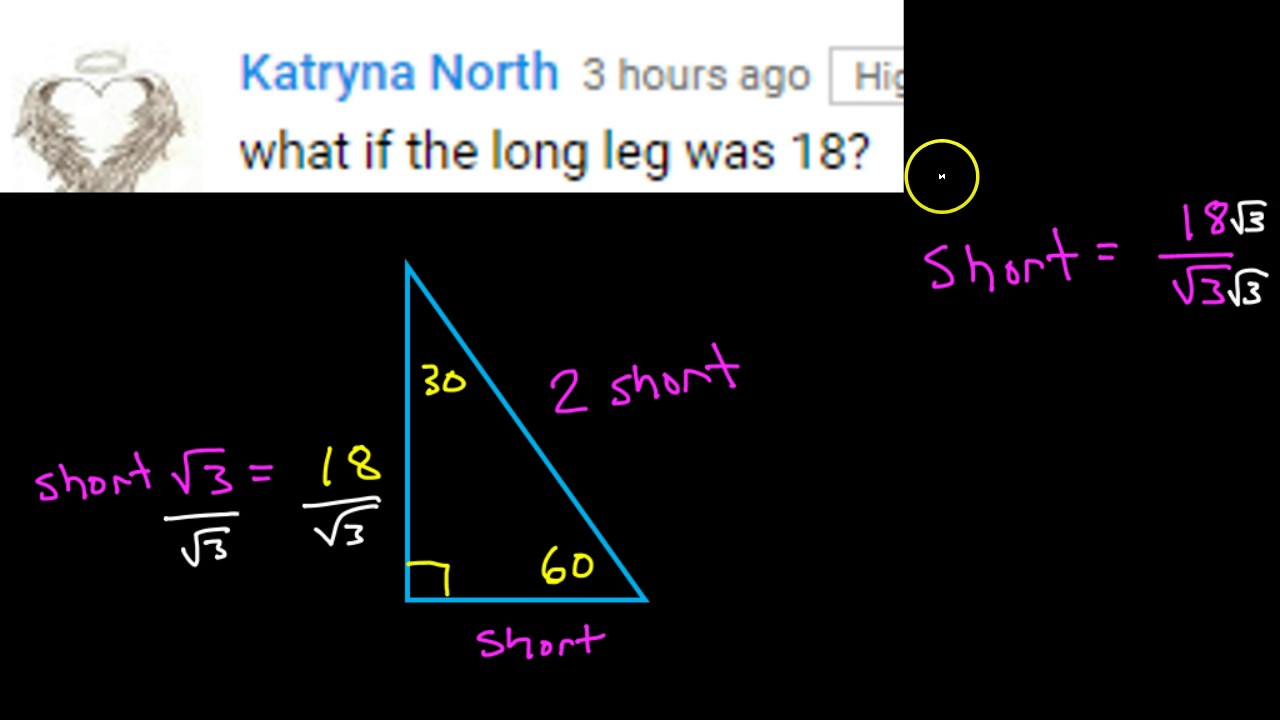



How Do You Solve A 30 60 90 Triangle If The Long Leg Is 18 Youtube



45 45 90 Right Triangles Solutions Examples Videos
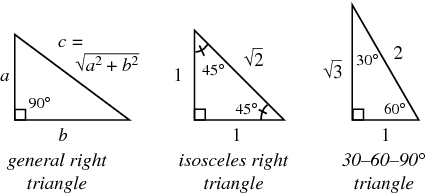



Right Triangle From Wolfram Mathworld
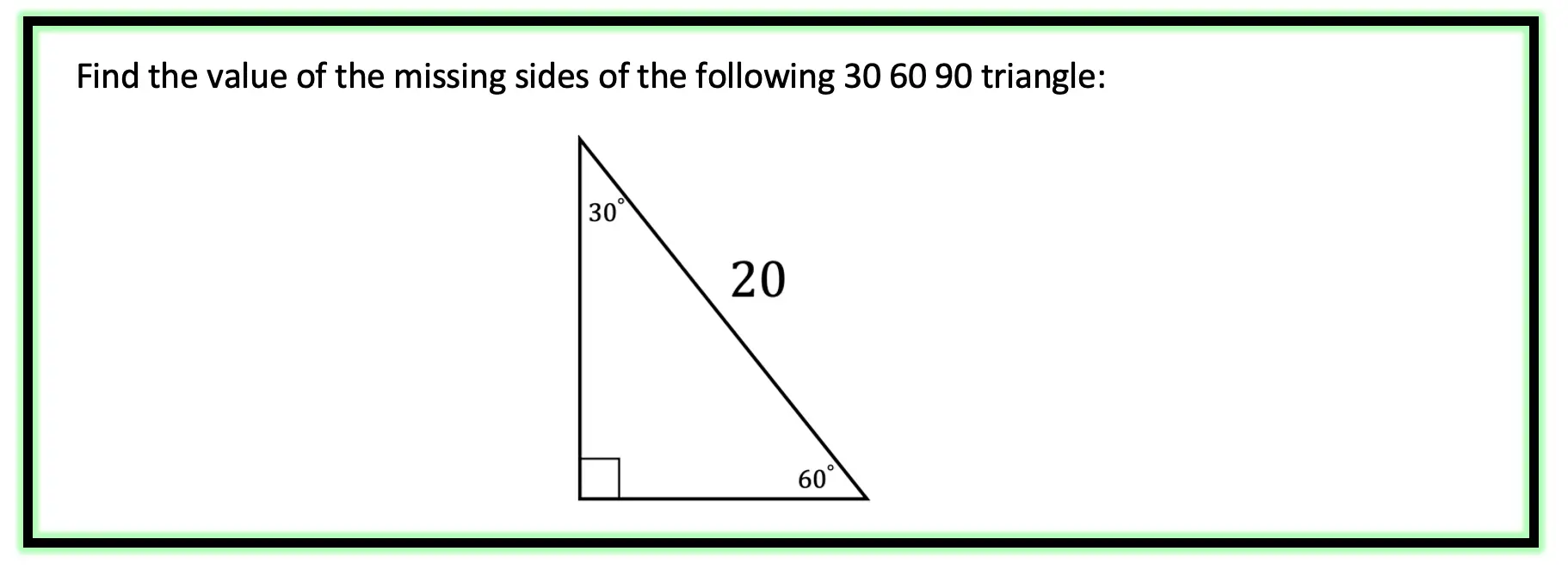



30 60 90 Special Triangles Geometry Mathsux 2



1
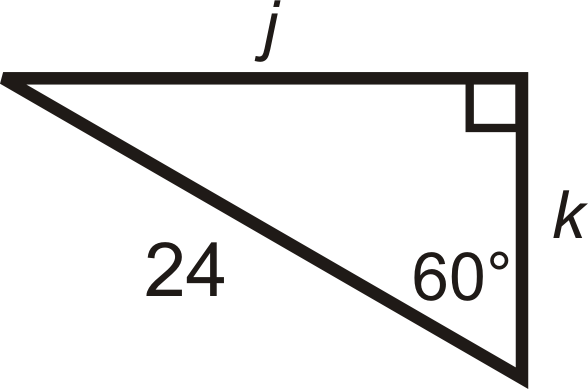



30 60 90 Right Triangles Ck 12 Foundation




How To Find The Length Of The Hypotenuse Of A Right Triangle Pythagorean Theorem Sat Math



0 件のコメント:
コメントを投稿